
- •IV. Пространства операторов
- •4. 1. Определение линейного оператора
- •4.2. Непрерывность
- •4.3. Обратный оператор
- •4.3 1. Замкнутость линейных операторов
- •4.3.2. Корректность компактных операторов
- •4.4. Пространства функционалов
- •4.4. Сопряжённые операторы
- •Продолжения операторов и функционалов
- •Культурный минимум.
- •Вопросы.
- •Задачи.
4.3 1. Замкнутость линейных операторов
Определение
1.
Линейный
оператор А,
действующий
из банахова
пространства
в банахово пространство
,
называется замкнутым,
если для любой последовательности
 и
такой, что
последовательность
и
такой, что
последовательность
 одновременно
с
последовательностью
одновременно
с
последовательностью
 ,причём
элемент
,причём
элемент
 ,
а элемент
.
,
а элемент
.
Комментарий.
Из определения следует, что если
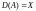 ,
то непрерывный линейный оператор всегда
замкнут (НЛО
всегда
ЗЛО:
“теорема о пришельцах”). Обратное,
вообще говоря, неверно. То есть существуют
замкнутые линейные операторы с областью
определения,
плотной в X,
которые
не являются непрерывными.
,
то непрерывный линейный оператор всегда
замкнут (НЛО
всегда
ЗЛО:
“теорема о пришельцах”). Обратное,
вообще говоря, неверно. То есть существуют
замкнутые линейные операторы с областью
определения,
плотной в X,
которые
не являются непрерывными.
Пример 1.
Покажем, что оператор дифференцирования
 не ограничен, если действует из
не ограничен, если действует из
 в
.
в
.
Пусть оператор
дифференцирования
 действует из
в
,
то есть
операторное уравнение имеет вид
действует из
в
,
то есть
операторное уравнение имеет вид
 .
Этот оператор определен не на всем
пространстве непрерывных функций, а
лишь на подпространстве непрерывных
функций, имеющих непрерывную производную.
Вообще, характерной особенностью
разрывных операторов является то, что
они не определены на всём пространстве.
В пространстве
норма
.
Этот оператор определен не на всем
пространстве непрерывных функций, а
лишь на подпространстве непрерывных
функций, имеющих непрерывную производную.
Вообще, характерной особенностью
разрывных операторов является то, что
они не определены на всём пространстве.
В пространстве
норма
 .
Возьмем из
последовательность
.
Возьмем из
последовательность
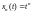 .
Она ограничена
в
:
.
Она ограничена
в
:
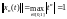 .
Рассмотрим
.
Рассмотрим
 .Тогда
.Тогда
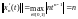 .
Таким образом, оператор
переводит ограниченное множество в
неограниченное, то есть этот оператор
не является ограниченным. Такая же
ситуация с последовательностью
.
Таким образом, оператор
переводит ограниченное множество в
неограниченное, то есть этот оператор
не является ограниченным. Такая же
ситуация с последовательностью
 .
В
.
В
 норма
норма
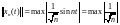 ,
а
,
а
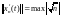 .
Тогда
.
Тогда
 ,
то есть
оператор дифференцирования
не ограничен,
то есть не является непрерывным. Это
значит, что прямая задача некорректна
на данной паре пространств
,
то есть
оператор дифференцирования
не ограничен,
то есть не является непрерывным. Это
значит, что прямая задача некорректна
на данной паре пространств
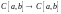 .
.
Но если в пространстве исходных данных выбрать более сильную норму, то ситуация изменится.
Рассмотрим
пространство
как пространство
 ,
а пространство
как пространство
,
а пространство
как пространство
 .
Тогда
.
Тогда
 Теперь
Теперь
 и задача дифференцирования стала
корректной, но на паре пространств
и задача дифференцирования стала
корректной, но на паре пространств
 .
.
На паре пространств
оператор
дифференцирования
является замкнутым, если область его
определения есть
 .
Действительно,
пусть последовательность
.
Действительно,
пусть последовательность
 в
в
 ,
,
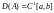 .
Тогда
последовательности
и
.
Тогда
последовательности
и
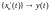 сходятся равномерно на сегменте
сходятся равномерно на сегменте и работает теорема о почленном
дифференцировании последовательности
функций. Отсюда
и работает теорема о почленном
дифференцировании последовательности
функций. Отсюда
 ,
то есть функция
,
то есть функция
 принадлежит области определения
оператора
и
принадлежит области определения
оператора
и
 .
Но это и означает замкнутость оператора
.
.
Но это и означает замкнутость оператора
.
Комментарий.
Заметим,
что хотя на паре пространств
прямая задача дифференцирования
корректна, обратная не корректна, так
как оператор
является
вырожденным. Его ядро нетривиально
и состоит из функций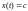 .
Чтобы найти
.
Чтобы найти
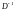 ,
нужно
для любой функции
,
нужно
для любой функции
 решить уравнение
решить уравнение
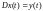 .
Но первообразная
непрерывной функции определяется с
точностью до постоянной
- элемента из
.
Но первообразная
непрерывной функции определяется с
точностью до постоянной
- элемента из
 оператора
.
Поэтому
обратный оператор не существует. Для
того чтобы он существовал, то есть задача
стала корректной, надо поставить задачу
Коши. Определим, например, оператор
на
подпространстве
оператора
.
Поэтому
обратный оператор не существует. Для
того чтобы он существовал, то есть задача
стала корректной, надо поставить задачу
Коши. Определим, например, оператор
на
подпространстве
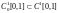 непрерывно
дифференцируемых функций
,
удовлетворяющих
условию
непрерывно
дифференцируемых функций
,
удовлетворяющих
условию
 .
Решение
этой задачи Коши
есть
.
Решение
этой задачи Коши
есть
 ,
тогда
,
тогда
 .
.
Определение
2.
Прямым
произведением
 линейных
пространств
и
называют множество
всех упорядоченных пар
линейных
пространств
и
называют множество
всех упорядоченных пар
 ,
,
 ,
причём
,
причём
 .
.
 произвольное число.
произвольное число.
Комментарий.
Нетрудно
видеть, что
 линейное пространство. Если
и
нормированные пространства, то
нормированное пространство с нормой
линейное пространство. Если
и
нормированные пространства, то
нормированное пространство с нормой
 .
.
Определение
3.
Пусть
оператор
действует
из банахова пространства
в
банахово пространство
.
Графиком
оператора
называется множество пар
 ,
то есть
,
то есть
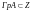 .
.
Определение
4.
Пусть
линейное многообразие пространства
.
График оператора
замкнут, если из того, что
 следует, что
,
а
.
следует, что
,
а
.
Таким
образом, линейный оператор
,
действующий
из
в
банахово пространство
,
замкнут,
если его график есть замкнутое линейное
подпространство пространства
 .
.
Теорема1. Пусть , где А – замкнутый линейный оператор, имеющий обратный оператор . Тогда также является замкнутым.
График
оператора
может быть получен из графика оператора
А
путем
''перестановки" точек:
 это одни и те же точки.
это одни и те же точки.
Пример
(продолжение).
Посмотрим теперь на оператор
дифференцирования
как на
обратный к оператору интегрирования
 ,
заданному на паре пространств
.
Равномерно сходящуюся последовательность
функций всегда можно почленно
интегрировать, то есть
,
заданному на паре пространств
.
Равномерно сходящуюся последовательность
функций всегда можно почленно
интегрировать, то есть


 и оператор интегрирования непрерывен.
Тогда по “теореме о пришельцах” он
замкнут. Обратным к нему является
оператор
дифференцирования, который замкнут
согласно
теореме1.
и оператор интегрирования непрерывен.
Тогда по “теореме о пришельцах” он
замкнут. Обратным к нему является
оператор
дифференцирования, который замкнут
согласно
теореме1.
Комментарий. Почти очевидно, что банахово пространство, если и только если и банаховы. Если , то НЛО всегда ЗЛО. Когда верно обратное?
Теорема2. (теорема Банаха о замкнутом графике). Пусть , где линейный оператор , отображающий всё банахово пространство на всё банахово пространство , имеет замкнутый график. Тогда - линейный непрерывный оператор.
1.
Покажем, что
 есть подпространство
.
Пусть
есть подпространство
.
Пусть
 и
и
 .
Тогда их линейная комбинация
.
Тогда их линейная комбинация
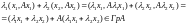 Поскольку оператор А – ЗЛО по условию,
то
замкнут в
,
то есть это подпространство.
Поскольку оператор А – ЗЛО по условию,
то
замкнут в
,
то есть это подпространство.
2. На подпространстве
 (замкнутое подпространство банахова
пространства само является банаховым
пространством)
(замкнутое подпространство банахова
пространства само является банаховым
пространством)
рассмотрим оператор
проецирования
 ,
действующий по правилу
,
действующий по правилу
 .
Это линейный
оператор, так как
.
Это линейный
оператор, так как
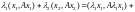
 Таким образом, оператор
биективно отображает банахово
пространство
на банахово пространство
.
Покажем, что он непрерывен:
Таким образом, оператор
биективно отображает банахово
пространство
на банахово пространство
.
Покажем, что он непрерывен:
 .
Тогда по
теореме
Банаха о гомеоморфизме существует
непрерывный линейный обратный оператор
.
Тогда по
теореме
Банаха о гомеоморфизме существует
непрерывный линейный обратный оператор
 :
:
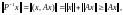 то есть
то есть
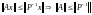 .
Тогда
линейный непрерывный оператор.
.
Тогда
линейный непрерывный оператор.
Комментарий. Для оператора , отображающего всё банахово пространство на всё банахово пространство , понятия замкнутости и непрерывности совпадают. Выясним, при каких условиях эти понятия совпадают, если .
Теорема3(Критерий замкнутости линейного оператора) Пусть , где пространства и банаховы. Линейный непрерывный оператор А замкнут, если и только если множество замкнуто.
Необходимость.
Пусть
оператор
НЛО и
множество
замкнуто. Покажем, что
замкнут. Рассмотрим последовательность
 .
Так как множество
замкнуто,
,
а из того, что оператор
непрерывен, следует, что
,
что и означает замкнутость оператора
.
.
Так как множество
замкнуто,
,
а из того, что оператор
непрерывен, следует, что
,
что и означает замкнутость оператора
.
Достаточность.
Пусть
оператор
НЛО и замкнут. Покажем, что множество
замкнуто. Пусть
,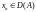 ,
а
- предельная точка
.
Тогда
,
а
- предельная точка
.
Тогда ,
то есть последовательность
,
то есть последовательность
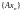 фундаментальна. Так как пространство
банахово, то последовательность
,
а из замкнутости оператора
следует, что
.
фундаментальна. Так как пространство
банахово, то последовательность
,
а из замкнутости оператора
следует, что
.
