2.Объем тела вращения

Пусть функция непрерывна на отрезке . В этом случае объем тела образованного вращением вокруг оси криволинейной трапеции, ограниченной графиком функции , прямыми , и осью абсцисс, может быть найден по формуле:

. (3)

Пример 2. Вычислить объем тела, полученного вращением фигуры, ограниченной параболой и прямой , вокруг оси абсцисс.

Графиком функции является парабола , вершина которой лежит в точке (1,1), а ветви параболы направлены вниз. Точки пересечений кривой с осью следующие .

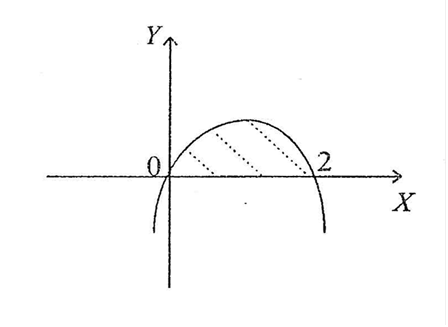
Отсюда по формуле (3) имеем

3) Длина дуги кривой

Пусть кривая задана непрерывной функцией , которая имеет на отрезке непрерывную производную . Тогда длина дуги линии от точки , до точки равна

.

Пример 3. Найти длину дуги линии от точки до точки .

Так как , то

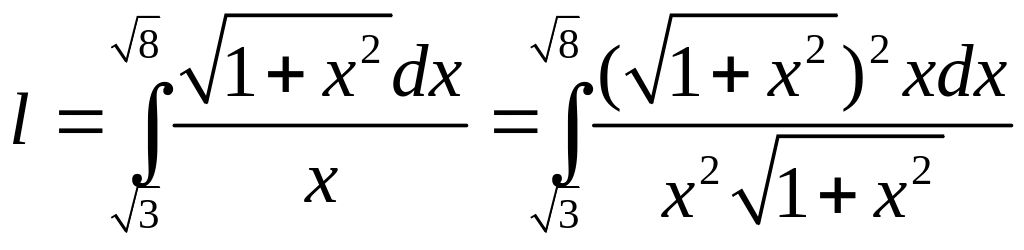
Здесь рекомендуется сделать замену переменной Тогда и пределы интегрирования изменяются следующим образом:

В результате получаем

Вставить ряды

1. Основные понятия

Пусть дана некоторая числовая последовательность

Выражение называется числовым рядом и может считаться обобщением понятия суммы на случай бесконечного числа слагаемых. Числа называются членами ряда, - общим членом ряда.

Сумма конечного числа первых членов ряда называется n-ной частичной суммой ряда. Ряд называется сходящимся, если при последовательность имеет конечный предел . При этом число называют суммой ряда и пишут .

Если последовательность не имеет конечного предела при , то ряд называется расходящимся и его сумма не определена.

Пример 1.1.

Вычислить сумму ряда или доказать его сходимость:

Решение. Воспользуемся тождеством:

для упрощения каждого слагаемого в частичной сумме :

И вычислим предел .

Ответ: ряд сходится и его сумма

1.2 Свойства сходящихся рядов

Если ряд сходится, то удаление или добавление любого конечного числа членов ряда не влияет на факт его сходимости, а меняет только значение его суммы.

Если ряд сходится и его сумма равна , то ряд тоже сходится и его сумма равна .

Если сумма ряда равна , а сумма ряда равна , то ряды сходятся и их суммы равны .

Если ряд сходится, то его общий член стремится к нулю при . Отсюда вытекает, что если , то ряд расходится. Доказательства указанных свойств можно найти в [1-3].

Пример 1.2

Исследовать сходимость ряда:

Решение. Здесь

Ответ: ряд расходится.

В практических задачах довольно часто не удается найти точное значение суммы ряда. В этом случае приближенно считают , выбирая n достаточно большим, можно найти значение с любой нужной точностью. Важно только знать, что существует т.е., что ряд сходится. Это можно проверить с помощью признаков сходимости- расходимости рядов.

1.3 Признаки сходимости положительных рядов

Пусть дан ряд с положительными членами . Предположим, что существует предел . Тогда, если , то ряд сходится, а если , то ряд расходится (радикальный признак Коши).

Замечание: если , то признак Коши не дает ответа на вопрос о сходимости ряда.

Пример 1.3

Исследовать сходимость ряда где и .

Решение : .

Ответ: При ряд сходится; при ряд расходится. При ряд расходится, так как .

Пусть дан ряд с положительными членами . Предположим, что существует предел . Тогда, если , то ряд сходится, а если , то ряд расходится (признак Даламбера).

Замечание: если , то признак Даламбера не дает ответа на вопрос о сходимости ряда.

Пример 1.4

Исследовать сходимость ряда

Решение :

Ответ: ряд сходится.

Пусть дан ряд члены которого положительны и монотонно убывают . Предположим, что существует функция ,удовлетворяющая условиям:

А) определена и непрерывна при ;

Б) и монотонно убывает при ;

В) .

Тогда несобственный интеграл первого рода, определяемый соотношением , и данный ряд сходится или расходится одновременно (интегральный признак Коши).

Пример 1.5

Исследовать сходимость ряда .

Решение :

Вычислим несобственный интеграл в зависимости от значения а.

Если то , т.е. расходится.

Если , , т.е., сходится.

Если , то , т.е., расходится.

Ответ: ряд сходится при и расходится при .

Пусть даны два ряда с положительными членами и причем для всех n выполняется неравенство . Тогда из сходимости ряда (b) следует сходимость ряда (a); из расходимости ряда (a) следует расходимость ряда (b) (теорема сравнения).Если предел отношения общих членов рядов (a) и (b) является конечным, не равным нулю числом, то эти ряды одновременно или оба сходятся, или оба расходятся (признак сравнения в предельной форме). Доказательства перечисленных признаков приведены [1-3].

Пример 1.6

Исследовать сходимость ряда .

Решение: Сравним с расходящимся гармоническим рядом , который расходится.

.

Ответ: ряд расходится.