Лабораторна робота 10 Корекція. Пі–регулятор. Пд-регулятор

Мета роботи: навчитись виконувати процедуру синтезу ПІ- та ПД-регуляторів, визначати запаси стійкості системи, будувати її частотні характеристики.

Основнi теоретичнi відомості

Передавальна функція ПІ-регулятора має вигляд

,

де К_р –коефіцієнт пропорційної частини, а К_і- інтегральної відповідно.

Діаграму Боде для такого регулятора зображено на рис.10.1. З рис.10.1 видно, що цей регулятор є регулятором з відставанням по фазі.

Процедура синтезу ПІ-регулятора зводиться до наступного:

1. Коефіцієнт підсилення системи з передавальною

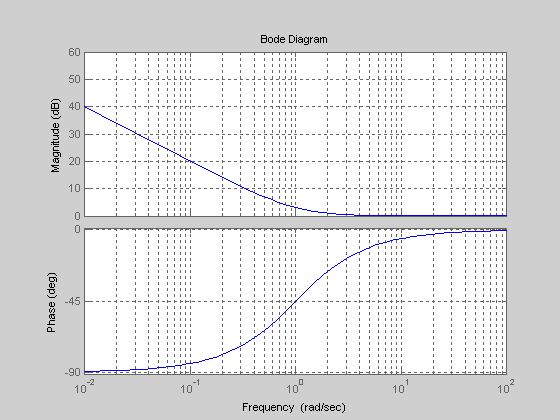
Рис .10.1. Діаграма Боде ПІ-регулятора

функцією змінити в К_с раз, для того щоб задовольнити вимоги до системи в області низьких частот.

1. Знайти частоту ₁, при якій

2. Визначити коефіцієнт К_р із виразу

3. Визначити абсолютне значення нуля передавальної функції

а потім

4. Далі передавальна функція регулятора буде мати вигляд

Ця процедура синтезу ПІ-регулятора ілюструється прикладом 10.1.

Приклад 10.1. Необхідно синтезувати пропорційно-інтегральний регулятор для системи, яка зображена на рис.9.1.

Передавальна функція некоректованої системи має вигляд:

, причому

Для некоректованої системи запас по фазі дорівнює 12, а запас по модулю – 3,5 дБ.

В пакеті MATLAB ці значення можна отримати за допомогою оператора margin. Ці значення є досить малими для системи.

Допустимо, що підсилення в області низьких частот задовольняє вимогам до системи, тому будемо рахувати, що К_с=1.

Припустимо, що запас по фазі повинен бути 50. Це означає, що при деякій частоті , на якій , повинна виконуватись умова .

Побудувавши діаграму Боде (див. рис.9.3), можна визначити що дана умова буде виконуватись на частоті .

Так як модуль частотної функції розімкненої системи на цій частоті приблизно дорівнює 4,55.Відповідно до пункту 3 процедури синтезу .

Відповідно до пункту 4 процедури синтезу та .

Тоді передавальна функція регулятора має вигляд

Передавальна функція ПД-регулятора має вигляд

,

де К_р –коефіцієнт пропорційної частини, а К_D- диференційної відповідно. Діаграму Боде для такого регулятора зображено на рис.10.2. З рис.10.2 видно, що цей регулятор є регулятором з попередженням по фазі.

Процедура аналітичного синтезу ПД-регулятора зводиться до наступного:

1. Для синтезу ПД-регулятора необхідно спочатку задати початкові дані: запас по фазі , коефіцієнт підсилення регулятора а_0,, та час встановлення перехідної характеристики .

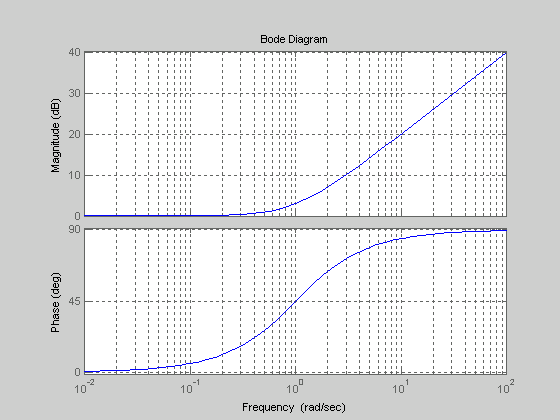
Рис. 10.2. Діаграма Боде ПД-регулятора

2. Обчислити частоту ₁, при якій

за формулою

3. Обчислити фазовий здвиг регулятора на частоті ₁

4. Передавальна функція регулятора буде мати вигляд

де , .

Обов’язково повинні виконуватись такі умови:

1.

2.

3. сos

Ця процедура синтезу ПД-регулятора ілюструється прикладом 10.2.

Приклад 10.2. Необхідно синтезувати пропорційно-диференційний регулятор для системи, яка зображена на рис.9.1. Передавальна функція некоректованої системи має вигляд:

, причому

Для синтезу ПД-регулятора необхідно спочатку задати початкові дані: запас по фазі , коефіцієнт підсилення регулятора а₀=1 та час встановлення перехідної характеристики =4с.

Подальші обчислення можна виконати в пакеті програм MATLAB:

1. Вводимо передавальну функцію та початкові значення:

Gp=tf([4],[1 3 2 0]); ph=50; a0=1; Ts=4;

w1=8/(Ts*tan(ph/57.296))

2. Відповідно до п.2 процедури синтезу вибираємо w1=1.7

3. Обчислимо значення модуля на частоті _1. Для цього використовуються оператори evalfr – обчислює значення комплексного коефіцієнта передачі для одного заданого комплексного значення частоти та abs - обчислює абсолютне значення.

Gpjw1=evalfr(Gp,j*w1)

Gpjw1mag=abs(Gpjw1)

4. Обчислимо фазовий здвиг регулятора на частоті ₁. Для цього використовуються оператор angle – обчислює значення кута при заданому значенні частоти

theta=-pi+ph/57.296-angle(Gpjw1)

5. Пункт 3 та 4 можна також виконати за допомогою відомих з попередніх робіт операторів :

[Gpjw1mag, PHASE] = BODE(Gp,1.7)

theta=-pi+ph/57.296- PHASE/57.296

6. Обчислимо значення коефіцієнтів а1 та b1:

a1=(1-a0*Gpjw1mag*cos(theta))/(w1*Gpjw1mag*sin(theta))

b1=(cos(theta)-a0*Gpjw1mag)/(w1*sin(theta))

7. Отримаємо передавальну функцію ПД- регулятора

Gc=tf([a1/b1 a0/b1],[1 1/b1])

8. Порахуємо передавальну функцію системи, яка замкнена зворотнім від’ємним одиничним зв’язком:

T=minreal(Gc*Gp/(1+Gc*Gp))

9. Щоб перевірити стійкість системи обчислимо полюси замкненої системи та запаси її стійкості:

pole(T); margin(Gc*Gp)

Щоб зробити висновки про отримані результати, необхідно побудувати перехідні характеристики отриманих замкнених систем з ПІ-регулятором та ПД-регулятором. Це можна зробити за допомогою оператора step: t=0:0.2:20; step(Т1,Т,t)

Завдання

Необхідно синтезувати пропорційно-інтегральний та пропорційно-диференційний регулятори для системи, яка зображена на рис.9.1. Передавальна функція некоректованої системи має вигляд:

, причому Для цього необхідно:

1. Визначити запас стійкості заданої системи.

2. По заданому алгоритму синтезувати ПІ-регулятор.

3. Визначити запас стійкості коректованої системи.

4. Побудувати її перехідну характеристику.

5. По заданому алгоритму синтезувати ПД-регулятор.

6. Визначити запас стійкості коректованої системи.

7. Побудувати її перехідну характеристику.