
- •Лабораторна робота 7 Визначення границi стiйкостi для неперервних систем управлiння
- •Основні теоретичні відомості
- •Лабораторна робота 8 Визначення границi стiйкостi для дискретних систем управлiння
- •Основнi теоретичнi відомості
- •Лабораторна робота 9 Корекція шляхом зміни коефіцієнта підсилення
- •Основнi теоретичнi відомості
- •Лабораторна робота 10 Корекція. Пі–регулятор. Пд-регулятор
- •Основнi теоретичнi відомості
- •Лабораторна робота 11 Синтез під-регулятора
- •Основнi теоретичнi відомості
- •Основні теоретичні відомості
- •Хід роботи
- •Контрольні запитання
- •Лабораторна робота 13 Поняття білий шум. Формуючий фільтр
- •Основні теоретичні відомості
- •Завдання
- •Контрольні запитання
- •Лабораторна робота 14 Структурний синтез. Аналітичне конструювання оптимального детермінованого регулятора для неперервних систем
- •Основні теоретичні відомості
- •Хід роботи
- •Контрольні запитання
- •Лабораторна робота 15 Структурний синтез. Аналітичне конструювання оптимального детермінованого регулятора для дискретних систем
- •Основні теоретичні відомості
- •Хід роботи
- •Контрольні запитання
Лабораторна робота 7 Визначення границi стiйкостi для неперервних систем управлiння
Мета роботи: навчитись визначати границi стiйкостi для неперервних систем управлiння, обчислити стiйкiсть неперервної системи за допомогою критерiю Гурвіца
Основні теоретичні відомості
При аналізі та синтезі неперервних систем управління велике значення має їх стійкість. Система є стійкою, якщо при обмеженому вхідному сигналі її вихідний сигнал є також обмеженим. Стійкість замкненої системи безпосередньо пов’язана із місцезнаходженням коренів її характеристичного рівняння. Неперервна система є стійкою, якщо всі корені характеристичного рівняння є від’ємними, тобто знаходяться в лівій півплощині на комплексній площині.
У пакеті MATLAB оператор roots використовується для розрахунку коренів характеристичного рівняння; оператор pole використовується для розрахунку полюсів системи; оператор pzmap використовується для графічного зображення нулів та полюсів системи на комплексній площині.
Приклад
7.1.
Система
представлена характеристичним рівнянням
![]() .
Визначити
стійка чи нестійка система.
.
Визначити
стійка чи нестійка система.
Розв’язання. Відразу видно, що задана система є нестійкою, оскільки вона має 3 додатні та 1 від’ємний коефіцієнти. Використовуючи пакет програм MATLAB, визначимо корені характеристичного рівняння.
p=[1 2 3 -1]; r=roots(p)
В результаті отримали третій корінь додатнім, тобто він розміщується в правій півплощині на комплексній площині, тож система є нестійкою.
Приклад
7.2.
Визначити
чи стійка система, яка задана передавальною
функцією
![]() .
.
Розв’язання. Вирішити дане завдання можна, використавши пакет програм MATLAB:
W=tf([1],[1 2 3 1]); p=pole(W); pzmap(W)
Отримаємо результат: p = -0.7849 + 1.3071i; -0.7849 - 1.3071i ;-0.4302
та графік розміщення нулів та полюсів на комплексній площині. Всі полюси розміщуються в лівій півплощині, тобто система є стійкою.
Стійкість
неперервної системи можна визначити
методом Гурвіца. Цей метод
дозволяє визначити число коренів
характеристичного рівняння, що розміщені
в правій півплощині. Розглянемо його
детальніше.
Нехай
характеристичне рівняння системи
![]() -го
порядку має вигляд:
-го
порядку має вигляд:
![]()
Для того, щоб система була стійка, необхідно щоб виконувалась умова, що визначник матриці Гурвіца і визначники всіх її діагональних мінорів повинні бути додатними. Матриця Гурвіца має вигляд:
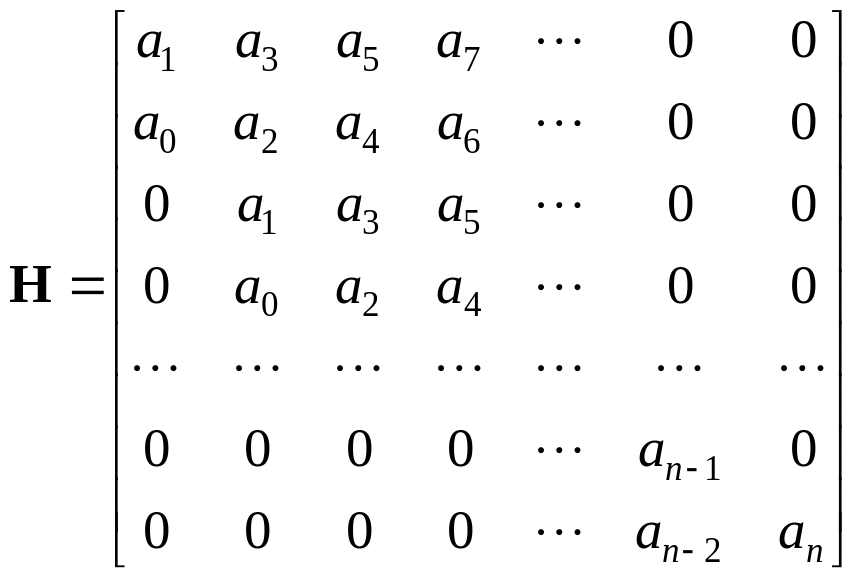 .
.
Основна
діагональ матриці Гурвіца представлена
коефіцієнтами характеристичного
рівняння, починаючи з
![]() і закінчуючи
і закінчуючи
![]() .Умови
критерію Гурвіца:
.Умови
критерію Гурвіца:
Якщо характеристичне рівняння системи має вигляд
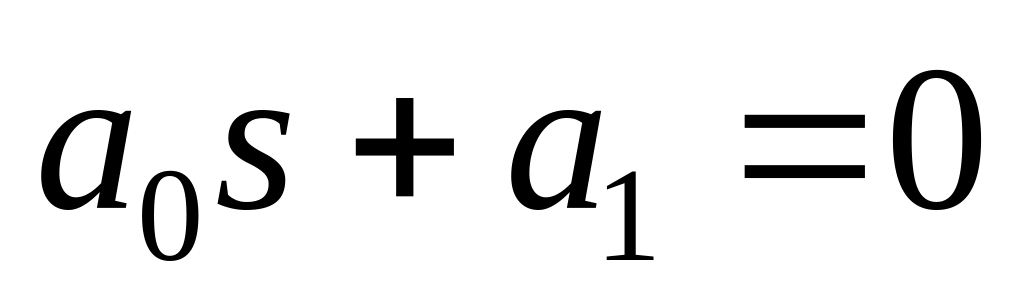 ,
то система стійка, коли
,
то система стійка, коли
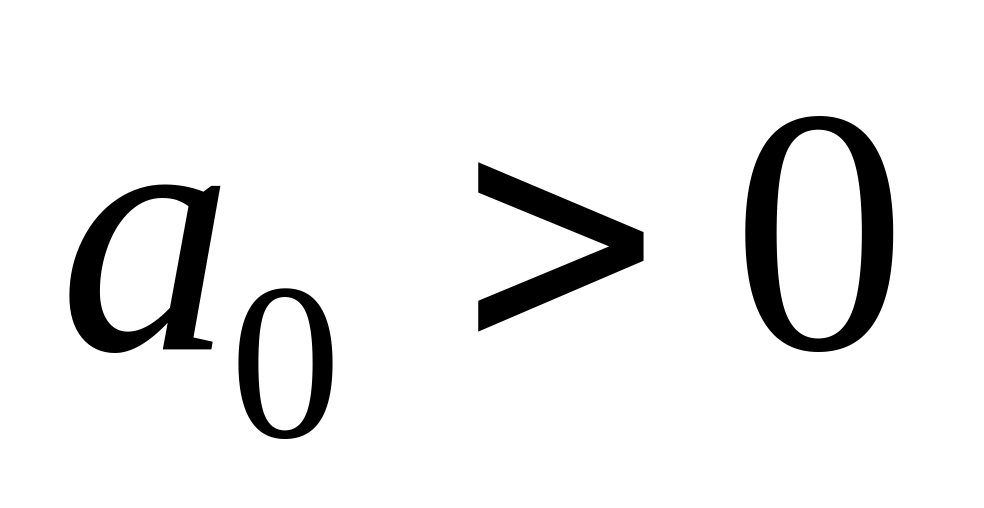 і
і
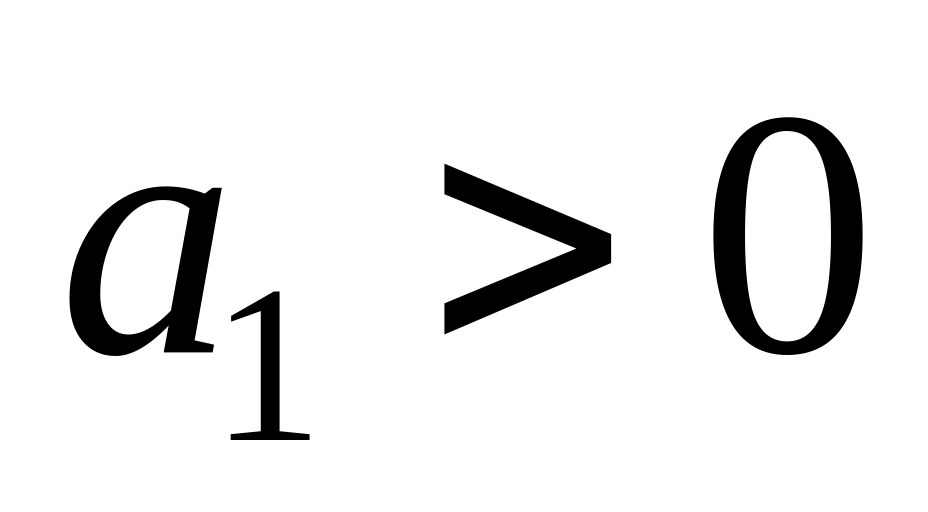 .
.Якщо характеристичне рівняння системи має вигляд
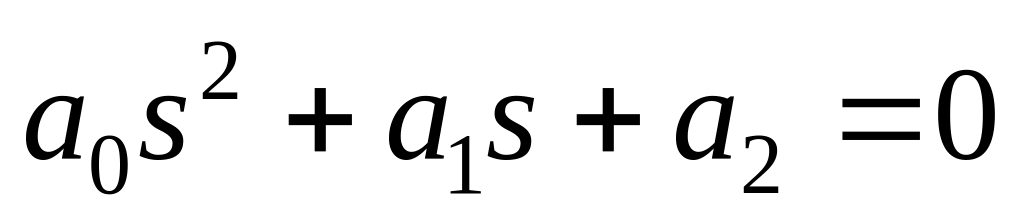 ,
то система стійка, коли
,
,
,
то система стійка, коли
,
,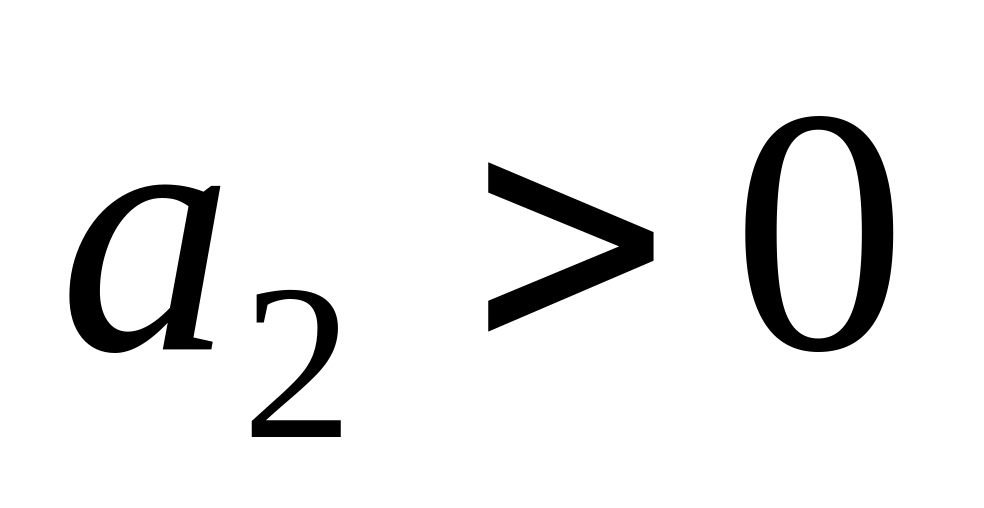 .
.Якщо характеристичне рівняння системи має вигляд
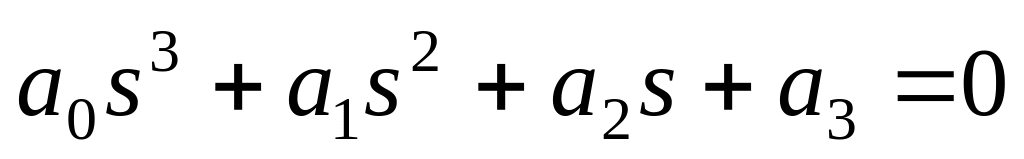 ,
то система стійка, коли
,
,
,
то система стійка, коли
,
,
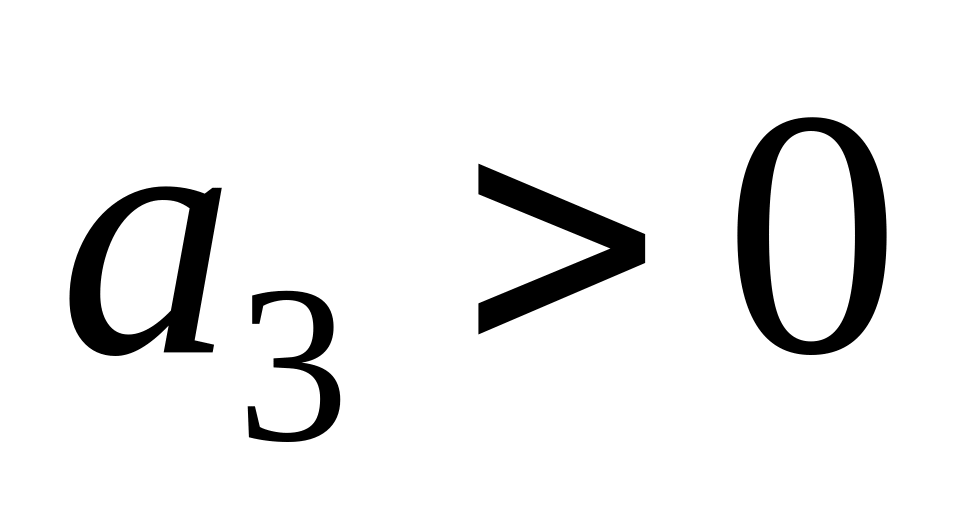 ,
,
,
,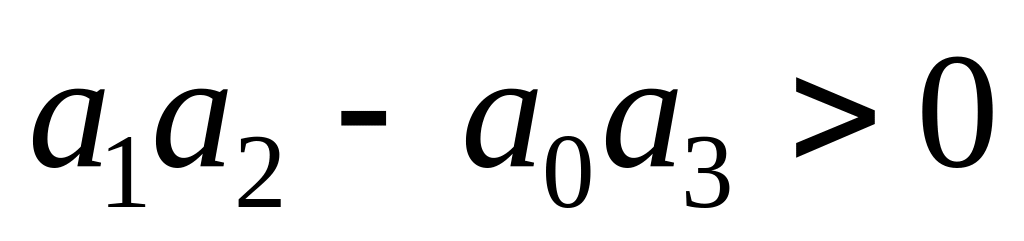 .
.Якщо характеристичне рівняння системи має вигляд
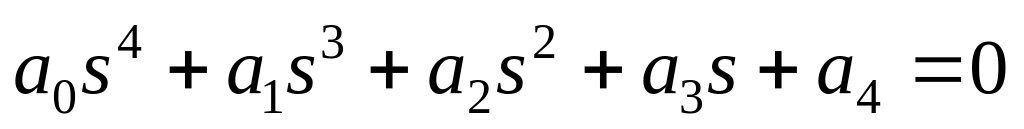 ,
то система стійка, коли
,
,
,
,
то система стійка, коли
,
,
,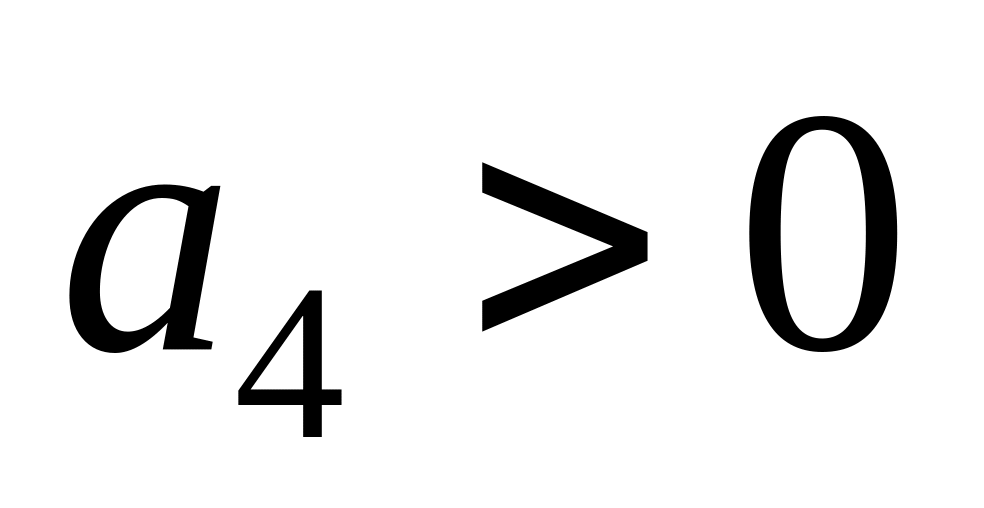 ,
,
,
,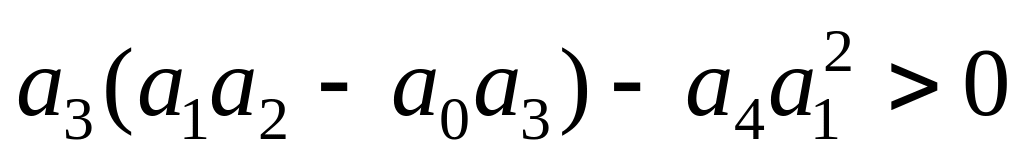 .
.
Приклад 7.3. Характеристичне рівняння системи
![]() .
.
При якому значенні К система буде стійкою?
Розв’язання. Система стійка, якщо
![]()
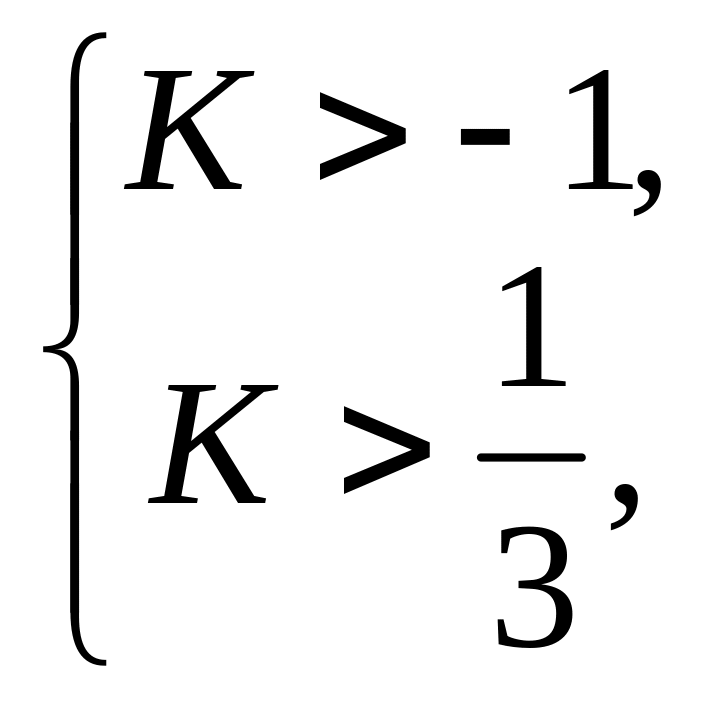
![]() Отже,
система стійка, якщо
Отже,
система стійка, якщо
![]() .
.
Критерій Гурвіца є алгебраїчним критерієм. До графічних критеріїв відноситься критерій Найквіста. Відповідно до цього критерію, замкнена система буде абсолютно стійкою, якщо амплітудна характеристика розімкнутої системи не буде охоплювати точку (-1,0). Це є необхідною та достатньою умовою для того, щоб замкнена система була стійкою. Термін „абсолютно стійка система” означає, що система є стійкою при любому зменшенні коефіцієнта підсилення розімкненої системи. Замкнена система буде нестійкою, якщо амплітудна характеристика розімкнутої системи буде охоплювати точку (-1,0). Замкнена система буде знаходитись на границі стійкості, якщо амплітудна характеристика розімкнутої системи буде проходити через точку (-1,0).
