Преобразование градации в системе передачи изображения. Параметрическое или градационное преобразование.
Преобразования, случающиеся с сигналом в системе:
Преобразования можно разделить на две группы:
Динамический диапазон системы больше или равен динамическому диапазону оригинала. В этом случае потери сигнала будут минимальными.
Преобразования тут наблюдаются такие:
А) Линейное – с полным сохранением этого сигнала, с градиентом, равным единице.
Б) Сигнал выходной отличается по контрасту от входного, но сохраняется линейность передачи. авыхода = gавхода – как с понижением, так и с повышением контраста.
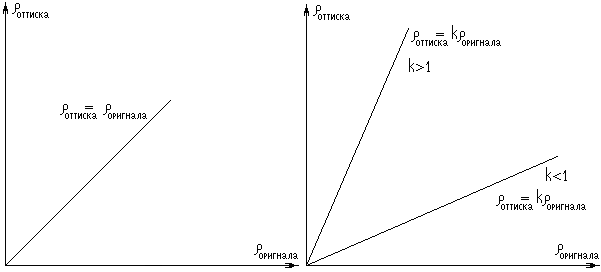
Линейная передача линейного сигнала или параметра - это истинно линейная передача; а линейная передача нелинейного параметра – это условно линейная передача.
Нелинейная передача. – когда входной сигнал преобразуется в выходной по какому-то закону.
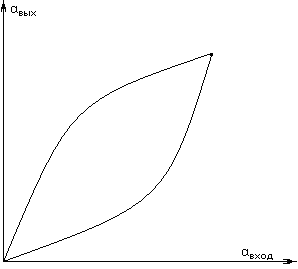
Кусочно-линейная передача. Передача осуществляется путем деления изображения на куски.
Часто кусочно-линейная передача аппроксимирует в нелинейную передачу.
Все детали сохраняются, но они могут быть преобразованы.
Рассмотрим тот случай, когда динамический диапазон системы меньше, чем диапазон изображения. В таком случае отсечка неизбежна.
Тогда можем сделать так: градиент уменьшаем, который можно осуществить по линейному или нелинейному закону различного типа.
Это случаи передачи сигнала с сохранением его мерности.
Если сигнал в оригинале и на выходе возрастает, то у этого позитива положительная полярность.
Если наоборот – на входе растет яркость, ьа на выходе падает, то мы имеем смену полярности – отрицательную полярность; у нас негатив.
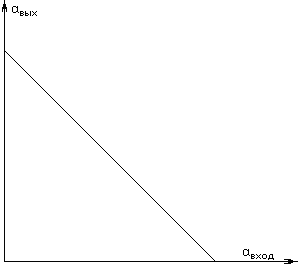
Возможности воспроизведения градации сигнала с использованием обратной связи.
Фильтр с обратной связью.
Можем получить так:
Часть сигнала, которую не можем из-за отсечки ввести, вводим при помощи изменения полярности.
Инерционность системы и фильтрация сигнала.
Понятие градации относится к большим деталям изображения. Но есть и достаточно мелкие детали, штрихи, а также границы.
Мы видим, что скачки – мелкие детали
границы и другие – передаются по-разному.
Если резкость высокая, то передается в
виде прямоугольного сигнала
; а если размыто, то сигнал имеет вид
.
Это из-за того, что все системы являются инерционными относительно скорости сигнала.
Свойство системы передавать резкие изменения сигнала как более плавные, сглаженные называется инерционность системы.
Инерционность системы влияет на ее структурные свойства.
Может быть пространственная инерционность, а может быть временная инерционность.
Наше пространственное изображение мы можем разбить на бесконечно большой набор точек. Если эти точки описывать математически, то мы можем получить дельта функцию или как называют ее функцию Дирака. Обозначают: δ-функция.
Функция Дирака описывает идеальное изображение.
Однако, если все это пропустить через систему, то мы получим не функцию Дирака, а функцию размытия точки:
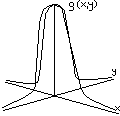
Каждая точка преобразуется (размывается) в пятно. И все изображение получается из наложений всех этих размытий.
Функция размытия точки – это характеристика всей системы.
Зная функцию размытия точки (ФРТ) и зная характер яркости и исходное наше изображение, мы можем рассчитать то, что мы получим на выходе системы.
Алгоритм расчета.
Для расчета мы переходим от функции размытия точки (ФРТ) к функции размытия линии (ФРЛ). Мы можем перейти от ФРТ к ФРЛ лишь в том случае, если наша система изотропна – она передается без изменений во все стороны – “размывается” кругом.
Для расчета мы переходим от ФРТ к ФРЛ.
Получаем при одномерном рассмотрении:
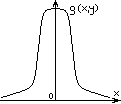
Функция размытия точки – это то распределение яркости или интенсивности, в которое превращается δ-функция в реальном изображении. Обычно эта функция размытия точки нормируется. Мы можем ее нормировать как g(x,y)=1. Или можно ее нормировать как
Все изображение состоит из таких функций размытия точки и если изображение выражено, определено в линейных величинах, то распределение интенсивности в любой его детали может быть найдено суммированием всех функций размытия точек в изображении взятых с тем весом, который определяется распространением интенсивности в изображении, заданным его градацией.