III. Динамика вращательного движения

-----------------------------------------------------------------------

1. Диск может вращаться вокруг оси, перпендикулярной плоскости диска и проходящей через его центр. К нему прикладывают одну из сил ( ,  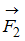,  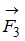 или  ), лежащих в плоскости диска и равных по модулю. Верным для угловых ускорений диска является соотношение …

	,

-----------------------------------------------------------------------

Решение: Согласно основному уравнению динамики вращательного движения твердого тела относительно неподвижной оси угловое ускорение равно:  . Отсюда следует, что угловое ускорение прямо пропорционально моменту приложенной к диску силы, который, в свою очередь, прямо пропорционален величине плеча силы (при условии равенства модулей сил). Таким образом,  ,  , так как плечо силы   равно нулю, и поэтому момент силы   равен нулю.

---------------------------------------------------------------------

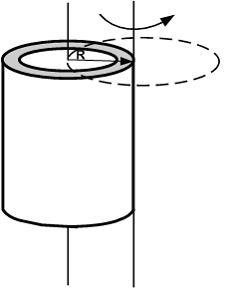
2. Если ось вращения тонкостенного кругового цилиндра перенести из центра масс на образующую (рис.), то момент инерции относительно новой оси _____ раза.

	увеличится в 2
	уменьшится в 2
	увеличится в 1,5
	уменьшится в 1,5

-----------------------------------------------------------------------

Решение: Момент инерции тонкостенного кругового цилиндра массы m и радиуса R относительно оси, проходящей через центр масс, вычисляется по формуле . Момент инерции относительно оси, проходящей через образующую, найдем по теореме Штейнера: . Тогда , то есть момент инерции увеличится в 2 раза.

---------------------------------------------------------------------

3. Диск радиусом 1 м, способный свободно вращаться вокруг горизонтальной оси, проходящей через точку О перпендикулярно плоскости рисунка, отклонили от вертикали на угол 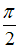  и отпустили. В начальный момент времени угловое ускорение диска равно _______ с^-2.

	7
	10
	5
	20

-----------------------------------------------------------------------

Решение: 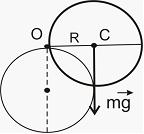Момент силы тяжести относительно оси, проходящей через точку О, равен  , где  радиус диска и плечо силы. Момент инерции диска относительно оси, проходящей через центр тяжести (точку С), равен  ; а момент инерции обруча относительно оси, проходящей через точку О, найдем по теореме Штейнера:  . Используя основной закон динамики вращательного движения твердого тела вокруг неподвижной оси, можем определить угловое ускорение:   .

---------------------------------------------------------------------

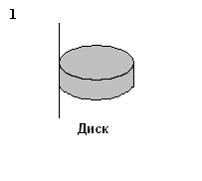
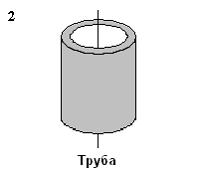
4. Рассматриваются три тела: диск, тонкостенная труба и сплошной шар; причем массы m и радиусы R шара и оснований диска и трубы одинаковы.  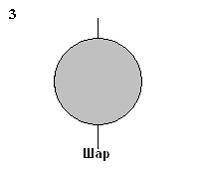Верным для моментов инерции рассматриваемых тел относительно указанных осей является соотношение …

-----------------------------------------------------------------------

Решение: Момент инерции сплошного однородного кругового цилиндра (диска) массы m и радиуса R относительно его оси  . Момент инерции диска относительно указанной оси вычисляется с использованием теоремы Штейнера:  . Момент инерции тонкостенного кругового цилиндра массы m и радиуса R относительно его оси  , момент инерции шара массы m и радиуса R  . Таким образом, правильным соотношением для моментов инерции рассматриваемых тел относительно указанных осей является соотношение  .

---------------------------------------------------------------------

5. Направления векторов момента импульса   и момента силы  для равнозамедленного вращения твердого тела правильно показаны на    рисунке …

	3
	1
	2
	4
	5

-----------------------------------------------------------------------

Решение: Момент  силы   определяется соотношением  , где   – радиус-вектор точки приложения силы. Направление вектора момента силы можно определить по правилу векторного произведения или по правилу правого винта (буравчика). Таким образом, момент силы направлен вдоль оси вращения. Согласно основному закону динамики вращательного движения твердого тела,  , где  момент инерции тела,  вектор углового ускорения, который сонаправлен с вектором момента силы. Момент импульса равен  , где  вектор угловой скорости, который по правилу правого винта направлен вдоль оси вращения, следовательно, и вектор момента импульса направлен так же. Поскольку вращение равнозамедленное,  вектор углового ускорения направлен противоположно вектору угловой скорости, значит, векторы   и   противоположны. Условию задачи соответствует рисунок 3.

---------------------------------------------------------------------

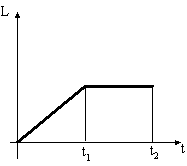
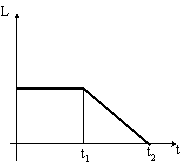
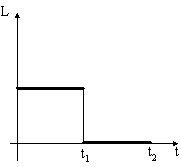
6. Диск начинает вращаться под действием момента сил, график временной зависимости которого представлен на рисунке:

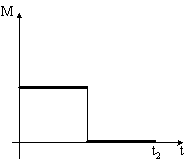Правильно отражает зависимость момента импульса диска от времени график …

-----------------------------------------------------------------------

Решение: Скорость изменения величины момента импульса относительно неподвижной оси равна величине суммарного момента внешних сил относительно этой оси.    где   – величина момента импульса,   – величина момента силы. Тогда величина момента импульса равна  . Вычислив интеграл от функции, характеризующей зависимость величины момента силы от времени, получим зависимость величины момента импульса от времени.

---------------------------------------------------------------------

7. Обруч скатывается без проскальзывания с горки высотой 2,5 м. Скорость обруча (в м/с) у основания горки при условии, что трением можно пренебречь, равна …

	5

---------------------------------------------------------------------

8. Величина момента импульса тела изменяется с течением времени по закону 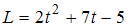(в единицах СИ). Если в момент времени 2 с угловое ускорение составляет 3 с^-2, то момент инерции тела (в кг*м²) равен …

	5
	6
	0,2
	0,5

-----------------------------------------------------------------------

Решение: Cкорость изменения величины момента импульса относительно неподвижной оси равна величине суммарного момента внешних сил относительно этой оси, то есть    где  – величина момента импульса,  – величина момента силы. Вычислив производную от функции, характеризующей зависимость величины момента импульса от времени, получим величину момента силы   . Используя основной закон динамики вращательного движения твердого тела вокруг неподвижной оси, можем определить его момент инерции:   .

-----------------------------------------------------------------------

9. Диск вращается вокруг неподвижной оси с постоянной угловой скоростью. В некоторый момент времени на диск начинает действовать не изменяющийся со временем тормозящий момент. Зависимость момента импульса диска от времени, начиная с этого момента, представлена на рисунке линией …

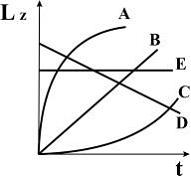
	D
	A
	B
	C
	E

-----------------------------------------------------------------------