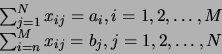22. Теория элитных групп.
Автор: профессор Ефимов.
Элита – группа элементов, которые по каким-либо признакам, критериям лучше, чем остальные (пример – космонавты по здоровью).
Элитная группа.
Генеральная совокупность – вне элитной группы.
Необходим критерий, который может быть комплексным, по которому отбирается подходит ли объект в элитную группу. При отборе может возникнуть ошибка.
Иногда при отборе присутствует рекомендатель – человек, который производит отбор в элитную группу. Здесь может быть субъективизм и ошибка может увеличиться.
Сорные элементы – не элитные элементы в элитной группе.
Рекомендатель иногда может пойти на ошибку сознательно. Например набирая себе на работу людей. Компания выступает в роле элитной группы. Рекомендатель – сам элемент элитной группы. Если сам рекомендатель отвечает всем критериям, то как правила все новые элементы будут приближаться к нему самому по критериям. Квалифицированный сотрудник не возьмет неквалифицированных. Но лучшие люди могут уходить из компании (в силу возврата или в другую компанию). И есть вероятность, что на место рекомендателя может попасть человек с не очень высокой квалификацией (может не уметь делать отбор). Он может увеличить процент проникновения сорных элементов в элитную группу, постепенно увеличивая их количество в элитно группе и элитная группа превращается не в элитную и деградирует.
Но не обязательно элитная группа должна вырождаться. Для этого следует внимательно отслеживать рекомендателей.
Процедура отбора – процедура типа «претендент – рекомендатель». Есть и другие типы процедур, например процедура «делегирования»
Способы управления элитной группой – «прополка» - удаление сорных элементов (пример - отчисление за неуспеваемость). Иногда приходится расставаться и с лучшими элементами элитной группы (они уходят выше). Процедура убытия лучших называется процедурой «снятия урожая».
23. Теория элитных групп и многокритериальность.
24. Транспортная задача.
В транспортной задаче требуется найти оптимальный план перевозок некоторого продукта от заданного множества производителей, также занумерованных числами 1, 2, …, М, к множеству потребителей, также занумерованных числами 1, 2, …, N.
Производственные возможности i-го производителя заданы объемом производимого продукта -ai. Спрос j-го потребителя на этот продукт задается числом bj.
Обозначим планируемый объем перевозок от i-го производителя к j-ому потребителю как xij. В этих условиях должны быть выполнены балансовые соотношения:
|
(6) |
Для существования допустимого плана перевозок должен выполнятся общий баланс между спросом и потреблением:
При
этом транспортную задачу называют
сбалансированной.
Можно убедиться, например, что в сбалансированной транспортной задаче xij=aibj/D (7)
являются допустимым вариантом перевозок, то есть удовлетворяющим ограничениям (6).
Целью решения транспортной задачи является минимизация суммарных транспортных расходов. Если предположить, что стоимость перевозки продукта линейно зависит от объема перевозки и характеризуется числами cij, где cij - стоимость перевозки единицы продукта от i-го производителя к j-му потребителю, а xij - объемы перевозок, то целевая функция в транспортной задаче принимает вид:
|
(8) |
и задача заключается в минимизации (8) при выполнении ограничений (6) и условия неотрицательности переменных xij.
Переменные xij можно представить в виде матрицы (см. табл. 1).
Таблица: Матрица объемов перевозок. |
||||||
|
1 |
2 |
... |
|
||
1 |
|
|
... |
|
||
2 |
|
|
... |
|
||
... |
... |
... |
... |
... |
||
M |
|
|
... |
|
||
Первое свойство матрицы называют разреженностью, а последнее свойство называют сверхразреженностью.
Для характеризации разреженности используют две меры - количество ненулевых элементов в матрице ограничений и их отношение к общему числу элементов матрицы. Последняя характеристика называется плотностью. Для транспортной задачи плотность d равна 3/(M+N) и падает с ростом размерности задачи, что вообще типично для задач линейного программирования.
Описанный вариант транспортной задачи называется транспортной задачей в матричной постановке. В такой задаче разрешаются связи между произвольными поставщиками и потребителями. На практике зачастую некоторые связи между определенными поставщиками и потребителями невозможны или нежелательны из-за разного рода внемодельных соображений (отсутствие дорог, специфика погрузочно-разгрузочного оборудования и тому подобное).
Наглядно транспортную задачу в сетевой постановке лучше всего представить в виде графа - некоторого множества вершин, соединенных дугами, обозначающими транспортные связи.