7.2. Методы расчета напряжений в однородных грунтах

Напряженное состояние в некоторой точке грунта характери­зуется совокупностью действующих в ней напряжений. Рассматри­вая в системе прямоугольных координат напряженное состояние элементарного кубика со сторонами, параллельными плоскостям координат (рис 7.2), различают следующие напряжения: _z— вертикальное нормальное напряжение; _y — горизонтальное нормаль­ное напряжение, действующее в направлении оси у; _x — горизон­тальное нормальное напряжение, действующее в направлении оси х; ґ_xy; ґ_yx — касательные напряжения, действующие по граням, парал­лельным оси z, равные между собой согласно правилу «парности напряжений»; ґ_xy; ґ_yx - равные касательные напряжения, действую­щие по граням, параллельным оси у; ґ_y; ґ_zy — равные касательные напряжения, действующие по граням, параллельным оси х.

Выражению для вертикальных нормальных напряжений может быть придан вид:

(7.1)

Величины безразмерного множителя К, зависящего от отношения r/z, приведены в табл. 7.1.

При малых значениях радиуса-вектора R напряжения получаются настолько большими, что грунт не мог бы их выдержать. Это след­ствие условности постановки задачи — приложение нагрузки в одной точке. В действительных условиях работы сооружений нагрузка всегда передается на грунт через площадки (фундаменты, колеса), распределяющие ее на некоторую площадь. Для вычисления возни­кающих в этом случае напряжений может быть использован метод суммирования напряжений от элементарных сил, распределенных по загруженной площадке. При этом предполагается, что грунты линей­но деформируемы, для них справедлив принцип независимости дейст­вия сил и что нагрузка свободно следует за проседающей поверх­ностью грунта, т. е. она приложена к абсолютно гибкому штампу.

Рис 7.3. Распределение вертикальных нормальных напряжений в грунтах от на­грузки, приложенной к гибкой бесконечной нагруженной полосе:

а — кривые распределения напряжений по горизонтальным сечениям на разных глубинах от поверхности грунта (надписи справа около кривых показывают глубину, выраженную в долях полуширины загруженной полосы);

б — кривые равных напряжений — изобары (надписи на кривых указывают напряжения в долях от давления на подошву полосы);

в — кривые распределения напряжений по глубине (надписи в нижней части графика указывают расстояние вертикалей, к которым относятся кривые, от оси, проходящей через середину полосы)

Определим напряжение в полупространстве, на часть поверхности которого Р, ограниченную некоторой замкнутой кривой, действует нагрузка, интенсивность которой изменяется по закону , где — интенсивность нагрузки в точке с координатами х и у. Если выделить внутри нагруженной площадки элемент (рис. 7.4), то давление на площадку dF будет равно f(х, у)dF. Вер­тикальное нормальное напряжение в точке полупространства А от элементарной силы, действующей на площадку dF:

, (7.2)

где R — расстояние от точки А до элементарной площадки dF.

Таблица 7.1. Значения К

r/z	К	r/z	К	r/z	К	r/z	К
0,00 0,05 0.10 0,16 0,20 0,30 0,40 0,50 0,60	0,4775 0,4746 0.4657 0,4482 0,4329 0,3849 0,3294 0,2733 0,2214	0,70 0,80 0,90 1,00 1,10 1,20 1,40 1,50 1,60	0,1762 0,1386 0,1083 0,0844 0,0658 0,0513 0,0317 0,0251 0,0200	1,70 1,90 2,00 2,10 2,30 2,40 2,50	0,0160 0,0105 0.0085 0,0070 0,0048 0,0040 0,0034	2,60 2,80 3,10 3,30 3,50 4,90	0,0029 0,0021 0,0013 0,009 0,0007 0,0001

Полное значение напряжений в точке А получается в результате интегри­рования выражения для d_z по всей на­груженной площад­ке F:

(7.3)

рис 7.4. Определение напряжений от нагрузки, приложенной к площадке произвольной формы.

Аналогично мо­гут быть найдены и другие составляю­щие напряжений.

Различают два случая расчета на­пряжений: 1) от на­грузок, приложен­ных к бесконечным полосам постоянной ширины и одинаково распределенных по длине и ширине полосы в любом сечении (длинные ленточные фундаменты, дорожные на­сыпи и плотины постоянного сечения), — плоская задача; 2) от на­грузок, распределенных по ограниченной площади (фундаменты зданий, башмаки колонн, опоры мостов, колеса и гусеницы транс­портных средств), — пространственная задача. В условиях плоской задачи для оценки напряженного состояния грунта достаточно ис­следовать распределение напряжений в любом сечении массива, перпендикулярном оси загруженной полосы. Исходными для реше­ния плоской задачи в различных случаях являются выражения для напряжений от элементарных сосредоточенных сил, распределенных но бесконечной линии — линейной нагрузки (задача Фламана)

При интенсивности нагрузки q (в кг/см) на единицу длины верти­кальное нормальное напряжение в точке А (х, у = 0, г) от силы qdy, приложенной к поверхности полупространства в точке М (х = 0; y, Z=0)

(7.4)

Полное значение вертикального нормального напряжения от всех сил, приложенных к загруженной линии:

(7.5)

Рис 7.5. Распределение напряжений от бесконечной линейной нагрузки

Другие наиболее часто используемые составляющие напряже­ния:

; (7.6)

Распределение напряжений от нагрузки, приложенной к беско­нечной полосе, находят аналогично. Пусть на поверхность упруго-изотропного массива действует нагрузка в виде бесконечной полосы, имеющей ширину В, причем нагрузка изменяется по ширине по не­которому закону р = f(х) (рис. 9.8, а}. Тогда нагрузка, приходящая­ся на бесконечно малый элемент ширины полосы dx:

(7.7)

По длине полосы элементарные нагрузки dp образуют бесконеч­ную линейную нагрузку, напряжения от которой определяются вы­ражениями 7.5 и 7.6.

Полное значение напряжений от нагрузки в виде полосы опреде­ляют интегрированием выражений для линейной нагрузки по ширине полосы. Так, вертикальные нормальные напряжения в какой-либо точке

(7.8)

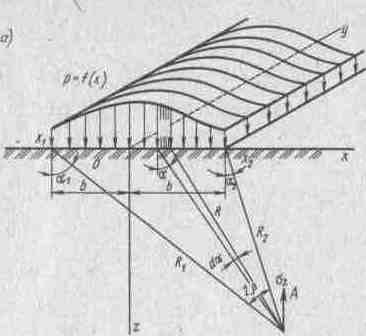
Рис 7.6. Распределение напряжений от загруженной полосы:

а — схема к выводу общей формулы; 6 — схема к определению напряжений в грунте, подстилающем насыпь