6.3 Сопротивление сыпучих грунтов сдвигу

В сыпучих грунтах силы сцепления практически отсутствуют или (в случае воздействия капиллярных сил) имеют временный харак­тер и исчезают при высыхании или полном водонасыщении грунта. Поэтому для несвязных грунтов уравнение (6.2) упрощается:

(6.11)

Коэффициент внутреннего трения несвязных грунтов зависит от крупности и формы частиц грунта, от его минералогического соста­ва, влажности и степени уплотнения.

Пески с остроугольными шероховатыми частицами обладают значительным внутренним трением, которое объясняется большой величиной неровностей на поверхности частиц и малым влиянием пленок связанной воды на характер этих неровностей. Изменение влажности песка практически не отражается на значении угла внутреннего трения, так как толщина водяных пленок весьма мала но .сравнению с неровностями на поверхности частиц и не может существенно влиять на зацепление взаимно перемещающихся ча­стиц. Наблюдаемое при испытаниях песков на сдвиг незначительное сцепление обычно объясняется присутствием в них пылеватых и глинистых частиц.

На сопротивление сдвигу несвязных грунтов оказывает суще­ственное влияние степень их уплотнения. При рыхлой укладке грун­товых частиц они легко могут смещаться при сдвиге относительно друг друга. В уплотненном грунте сдвигающейся частице приходит­ся преодолевать существенное сопротивление трению о шерохова­тые поверхности смежных частиц и сопротивление частиц раздвиганию. В процессе сдвига несвязных грунтов в зоне взаимных смещений грунтовых частиц устанавливается некоторое постоянное для каждого грунта значение пористости, названное Н. М. Герсевановым критической пористостью. Грунты, имеющие пористость меньше критической, при сдвиге разрыхляются, а более рыхлые грунты уплотняются, что видно из рис 6.2, б (кривая 2).

Значения углов внутреннего трения песчаных грунтов меняются для мелкозернистых и пылеватых грунтов от 26 до 30°, а у крупно­зернистых песков с включением гравия — от 30 до 35° в зависимо­сти от степени уплотнения. Горные пески с шероховатыми и остро­угольными зернами имеют больший коэффициент внутреннего' трения, чем речные и эоловые пески со скатанными зернами.

7. Напряжения в грунтах

7.1. Напряженное состояние грунтов

При рассмотрении задач, связанных с оценкой устойчивости грунтовых массивов и возведенных на них сооружений, необходимо знать, какие напряжения возникают в грунте при действии нагрузок. Без учета распределения напряжений в грунте невозможно, например, рассчитать осадки насыпей, устоев мостов, фундаментов искусственных сооружений на мягких основаниях, определить допустимую нагрузку от сооружения. Расчеты толщины и прочности дорожной одежды основываются на теории распределения напряжения в слоистых системах.

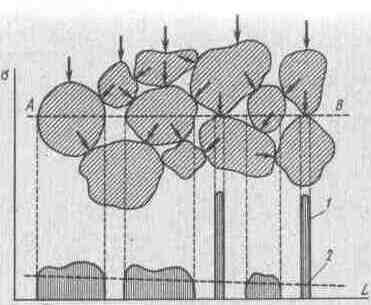
Давление от нагрузки, приложенной к поверхности грунтового массива, передается в грунте частицами или структурными агрегатами через точки контакта, распределяясь по мере углубления и грунт на все большую площадь. Среднее значение усилий, действующих на отдельные частицы, при этом уменьшается. Однако и напряжения в отдельных частицах и междучастичных связях в пределах какого-либо выделенного сечения (сечение АВ на рис 7.1) могут превышать их прочность и вызывать разрушение. При рассмотрении напряженного состояния грунта подобная местная концентрация напряжений не учитывается, так как она, отражаясь на условиях взаимного расположения отдельных частиц, не влияет на устойчивость грунтового массива в целом.

При оценке напряжений, действующих в грунтах, реальные силы, приложенные к отдельным грунтовым частицам, заменяют воображаемыми силами, распределенными по всему объему или сечению грунтового массива, в том числе и в промежутках между частицами. Величину этих сил, отнесенных к единице площади сечения массива, и принимают условно за величину напряжений и грунте. Это оправдывается тем, что размеры грунтовых частиц существенно малы по сравнению с размерами площадок, через которые давление от сооружений или транспортных средств передает­ся на грунт. Напряженное состояние грунтового массива при действии нагрузки, приложенной к его поверхности, связано со сте­пенью развития деформации (см. рис. 7.1). При воздействии по­степенно возрастающих нагрузок происходит изменение закономер­ностей распределения напряжений.

При относительно малых нагрузках и деформациях, соответст­вующих первой фазе деформации, когда зависимость «нагрузка - деформация» прямолинейна и грунт практически подчиняется закону Гука, напряженное состояние грунта близко к рассматриваемому в теории упругости. Однако при применении к грунтам решений теории упругости грунт рассматривают не как упругое, как линейно деформируемое тело. То обстоятельство, что деформации грунта не полностью упруги (т. е. не протекают мгновенно после приложения нагрузки и не восстанавливаются полностью после ее удаления), не имеет практического значения, поскольку в строитель­ной практике при возведении различ­ных сооружений приходится иметь дело обычно с одно­кратным приложени­ем нагрузки к грун­ту, без последующей разгрузки.

Проф. Н. М. Герсеванов доказал, что при анализе напря­женного состояния глинистых грунтов в основаниях сооруже­ний, когда интерва­лы изменения давле­ния до и после воздействия сооружения невелики, а напряжения малы, выводы теории упругости можно применять к грунтам в фундаментостроении с наименьшей обоснованностью, чем к стали при рас­чете деталей машин. Однако, применяя к грунтам зависимости теории упругости, не следует забывать, что они предусматривают постоянство или закономерность изменения свойств грунтов по глу­бине. Фактически грунтовые напластования, образовавшиеся в ре­зультате длительно протекавших геологических процессов, неодно­родны, что особенно приходится учитывать при расчетах осадок сооружений и допускаемых нагрузок на грунт.

Рис. 7.1. Напряжения в отдельных грунтовых частицах: 1— фактические напряжения в частицах грунта; 2 — среднее значение напряжений грунта

При превышении давлением на грунт некоторой предельной «критической» величины около краев штампа, передающего нагруз­ку, начинают возникать зоны пластических деформаций, которые, постепенно возрастая, распространяются в глубь грунта, захваты­вая все больший объем. Этот период работы грунта соответствует II фазе деформации. Наличие зон пластической деформации, в ко­торых грунт не может воспринять на себя ту же нагрузку, что до начала сдвигов, изменяет закономерности, которым подчиняется напряженное состояние грунта. В настоящее время разработано лишь несколько задач, рассматривающих напряженное состояние в грунте вблизи от штампа при частичном развитии зон пласти­ческих деформаций. Основные исследования в этом направлении выполнены проф. М. И. Горбуновым-Посадовым. При деформа­циях, относящихся к III фазе, напряженное состояние соответствует задаче предельного равновесия теории пластичности, решения ко­торой имеются также лишь для ряда частных случаев.

Рис 7.2. Напряженное состояние элементарного кубика грунта

Многочисленные экспериментальные работы показали, что при развитии в грунте пластических деформаций напряжения, измеренные вблизи от подошвы штампов и в верхних слоях не связных грунтов, отличаются от рассчитанных по формулам теории упругости, и совпадение между ними начинается лишь за пределами зоны распростра­нения пластических деформа­ций с глубин, равных 1...1.5 диаметра площадок, через ко­торые передается давление. На меньших глубинах факти­ческие напряжения по верти­кальной оси, проходящей через центр площадки, больше, чем вычисленные по формулам те­ории упругости, но более быстро уменьшаются по мере удаления от вертикальной оси в стороны. Происходит как бы концентрация напряжений вблизи линии дейст­вия нагрузки.

При определении напряжений от нагрузок, приложенных к. ма­лым площадкам — диаметром менее 1 м, используют формулы тео­рии упругости с введением в них поправочных коэффициентов кон­центрации. Следует отметить, что способ определения напряжений в грунтах методами теории упругости не является единственным.