5. Влияние кривизны Земли на вертикальные и горизонтальные расстояния.

Н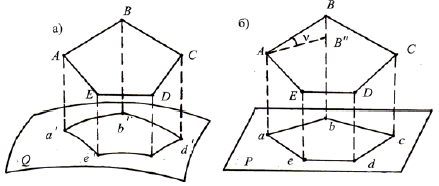 а рисунке показано ортогональное проектирование контура ABCDE земной поверхности на поверхность референц-эллипсоида и плоскость.

Как видно из рисунка, при ортогональном проектировании на рефе-ренц-эллипсоид проекцией многоугольника ABCDE будет сферический многоугольник a'b'c'd'e', а при ортогональном проектировании многоугольника ABCDE на плоскость его проекцией будет плоский многоугольник abcde, который называют горизонтальной проекцией участка местности.

Стороны плоского многоугольника ab, bc и т. д. являются горизонтальнымипроложениями соответствующих сторон пространственного многоугольника АВ, ВС и т. д. Как видно из рисунка, горизонтальное проложение линии всегда меньше наклонной длины линии на местности.

d = D cosν,

где ν – угол наклона линии местности к плоскости Р.

И зучение формы и размеров сферической проекции фигуры местности является более сложным, чем изучение плоской проекции, кроме этого сферическую проекцию нельзя изобразить в подобном виде на плоскости из-за влияния кривизны Земли.

Примем фигуру Земли за шар радиусом R. О – центр земного шара. Через точку А проведена горизонтальная плоскость, перпендикулярная к радиусу ОА. Разность между длиной касательной АС = d и длиной дуги АВ = D будет составлять погрешность в горизонтальном расстоянии при замене сферической поверхности плоскостью. Величина этой погрешности будет

Δd = d – D = D3/3R2

При R ≈ 6000 км и D = 10 км получим

Δd/D = D2/(3R2) = 102/(3 · 36 · 104) ≈ 1/106 = 1/1000000.

Такой погрешностью характеризуются наиболее точные измерения линий в геодезии. Следовательно, участки земной поверхности размером20×20 км можно считать плоскими, и в отношении расстояний, меньших20 км, сферическую проекцию участков местности можно принимать за плоскую.

Величина погрешности в вертикальном расстоянии, т. е. в высоте точки В, выразится отрезком ВС = h:

h = ОС – ОВ = d 2/2R.

Придавая d в формуле (3.5) различные значения и приняв R = 6000 км, получим: для d = 100 м – h = 1 мм, для d = 300 м – h = 8 мм, для d = 2000 м – h = 33,4 мм.

При строительстве инженерных сооружений погрешности высотных измерений не должны превышать 1–2 мм, поэтому влияние кривизны Земли на определение высоты должно учитываться уже для расстояний более 100 м.

6. Геодезические измерения. Единицы измерений.

Измерения- процесс сравнения какой-либо величины с другой однородной величиной, принимаемой за единицу.

Три вида измерений:

1. линейные — определяются расстояния между заданными точками;

2. угловые — определяются значения горизонтальных и вертикальных углов между направлениями на заданные точки;

3. высотные (нивелирование) — определяются разности высот отдельных точек.

За единицу линейных и высотных измерений (расстояний, высот и превышений) в геодезии принят метр.

Единицей для измерений углов (горизонтальных и вертикаль-

ных) служит градус, представляющий 1/90 прямого угла или 1/360 окружности. Градус содержит 60 угл. мин, минута делится на 60 угл. с. В некоторых странах применяют градовую систему, в которой 1 град составляет 1/400 окружности, градовая минута —

1/100 град, а градовая секунда — 1/100 град мин.

Измерения называют прямыми, если их выполняют с помощью приборов, позволяющих непосредственно сравнить измеряемую величину с величиной, принятой за единицу, и косвенными, когда искомую величину получают путем вычислений на основе результатов прямых измерений.

Необходимыми условиями любого измерения являются:

1. объект измерения;

2. субъект измерения — лицо, производящее измерение;

3. мерный прибор, которым выполняют измерения;

4. метод измерения — совокупность правил и действий, определяющих процесс измерения;

5. внешняя среда, в которой выполняют измерения.

Обозначенные на местности точки, от которых выполняют геодезические измерения, называются исходными. Точки, положениекоторых на местности необходимо определить, называют определяемыми.

Исходные и определяемые точки могут располагаться в горизонтальной плоскости в плане (плановые точки) и вертикальной — по высоте (высотные точки).