23. Средняя квадратическая ошибка измерения. Формула Гаусса. Абсолютная и относительная ошибки. Предельная ошибка.

Для правильного использования результатов измерений необходимо знать, с какой точностью, т.е. с какой степенью близостик истинному значению измеряемой величины, они получены. Характеристикой точности отдельного измерения в теории погрешностей служит предложенная Гауссомсредняяквадратическаяпогрешносьm, вычисляемая по следующей формуле:

где n — число измерений данной величины.

Эта формула применима для случаев, когда известно истинное значение измеряемой величины. Такие случаи в практике встречаются редко. В то же время из измерений можно получить результат, наиболее близкий к истинному значению, — арифметическую средину. Для этого случая средняя квадратическая погрешность одного измерения подсчитывается по формуле Бесселя:

где δ — отклонения отдельных значений измеренной величины от арифметической средины, называемые вероятнейшими погрешностями, причем [δ] = 0.

Точность арифметической средины, естественно, будет выше точности отдельного измерения. Ее средняя квадратическая погрешность определяется по формуле

,

где m — средняя квадратическая погрешность одного измерения, вычисляемая по двум предыдущим формулам.

Часто в практике для контроля и повышения точности определяемую величину измеряют дважды — в прямом и обратном направлениях, например, длину линий, превышения междуточками. Из двух полученных значений за окончательное принимается среднее из них. В этом случае средняя квадратическая погрешность одного измеренияа

,

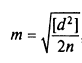а среднего результата из двух измерений

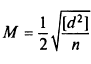
где d — разность двукратно измеренных величин; n — число разностей (двойных измерений).

В соответствии с первым свойством случайных погрешностейдля абсолютной величины случайной погрешности при данныхусловиях измерений существует допустимый предел, называемыйпредельной погрешностью. В строительных нормах предельная погрешность называется допускаемым отклонением.

Теорией погрешностей измерений доказывается, что абсолютное большинство случайных погрешностей (68,3%) данного рядаизмерений находится в интервале от 0 до ±m в интервал от0 до ±2m попадает 95,4 %, а от 0 до ±3m — 99,7 % погрешностей.

Таким образом, из 100 погрешностей данного ряда измеренийлишь пять могут оказаться больше или равны 2m, а из 1000погрешностей только три будут больше или равны 3m.

На основании этого в качестве предельной погрешности Δ_пр для данного ряда измерений принимается утроенная средняя квадратическая погрешность, т.е. Δ_пр = 3m. На практике во многих работахдля повышения требований точности измерений принимают

Δ_пр = 2m. Погрешности измерений, величины которых превосходят Δ_пр, считают грубыми.

Иногда о точности измерений судят не по абсолютной величине средней квадратической или предельной погрешности, а повеличине относительной погрешности.

Относительной погрешностью называется отношение абсолютной погрешности к значению самой измеренной величины. Относительную погрешность выражают в виде простойдроби, числитель которой — единица, а знаменатель — число,округленное до двух-трех значащих цифр с нулями. Например,относительная средняя квадратическая погрешность измерениялинии длиной l = 110 м при m₁= 2 см равна m₁/I = 1/5500, аотносительная предельная погрешность при Δ_пр = Зm = 6 см

Δ_пр/1 — 1/1800