3. Дифракция света.

3. 1. Принцип Гюйгенса-Френеля.

Если свет от источника через сферическое отверстие на­править на экран (рис. 3.1 а), то, согласно закону прямолиней­ного распространения света, на экране должно наблюдаться светлое пятно АВ - изображение отверстия. При уменьшении отвер­стия его изображение также должно уменьшаться. Однако опыт привел к неожиданному результату: начиная с определенного размера отверстия его дальнейшее уменьшение сопровождается увеличением пятна (А’B’), которое становится расплывчатым, нерав­номерно освещенным и на нем появляется ряд колец (рис. 3.1 б). Данное явление проникновения световых волн в область гео­метрической тени, огибания ими препятствий и вообще откло­нение их от прямолинейного распростра­нения было названо диф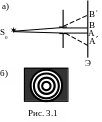 ракцией света. Дифракция явилась еще од­ним подтверждением справедливо­сти волновой теории света.

Изложенный в разделе 2. 1. принцип Гюйгенса помог объяснить дифракцию качественно. Поскольку вторичные источники излучают сферические волны, световое воз­мущение будет распространяться по всем направлениям. Значит, каждая точка отверстия (рис. 3.1 a) будет источником сферической волны и свет за отверстием мо­жет идти по всем направлениям, т.е. отклоняться от прямоли­нейности. Французский физик О. Френель, развивая идеи Гюй­генса, дал метод количественного расчета дифракции, назван­ный принципом Гюйгенса-Френеля. Рассмотрим основные поло­жения данного принципа:

1. Любой источник света S₀ можно заменить эквивалент­ной системой фиктивных (вторичных) источников, находящихся на какой-либо его волновой поверхности S.

2. Все вторичные ис­точники вол­новой поверхности S излучают коге­рентные волны, которые накладываются во всех точках пространства и интерферируют между собой.

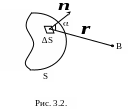
3. Каждый вторичный источник излучает преимущественно в направлении внешней нормали n к dS. Амплитуда вторичной волны в на­правлении r (где r – расстояние от dS до точки наблюдения В) уменьшается с увеличением угла α между r и нормалью n к dS (рис. 3.2). Она становится равной нулю при α ≥ π/2, т.е. излучение внутрь поверхности не распространяется. От каждого участка dS в точку В приходит световое колебание

.

Здесь Е₀ – амплитудное значение светового вектора, С(α)- коэффициент, зависящий от угла α (С(0) = 1, С(π/2)= 0). Тогда результирующий световой вектор от всей волновой поверхности S в точке В равен

.

Данный интеграл по поверхности называют интегралом Френеля. Современная теория Максвелла электромагнитных волн для точного решения задачи о распространении световых волн при наличии препятствий приводит к выражению аналогичному интегралу Френеля. Это математическое выражение позволяет вычислять световое возмущение в любой точке наблюдения. Недостатком данного принципа явля­ется сложность его практического применения.

4. Если часть волновой поверхности закрыть непрозрач­ным экраном, то вторичные волны излучаются только откры­тыми участками поверхности.

3 . 2. Метод зон Френеля.

Для упрощения расчета результирующей амплитуды све­тового колебания в точке наблюдения Френель предложил ме­тод деления фронта волны на зоны. Пусть S– точечный источ­ник света, P – произвольная точка наблюдения, в которой необ­ходимо определить амплитуду Е световых колебаний. Фронт волны в опре­деленный мо­мент времени есть сфера S’ (рис. 3.3). Зоны Френеля стро­ятся таким обра­зом, что рас­стояния от краев двух соседних зон до точки на­блюдения отли­чаются на половину длины световой волны λ/2. Обозначим расстояние от точки P до волнового фронта OP = L, тогда границей централь­ной или первой зоны будут точки поверхности S’, находящиеся на расстоянии L+λ/2 от точки P. Эти точки расположены на по­верхности по окружности. Точки сферы S’, находящиеся на рас­стоянии L+2λ/2 от P, образуют границу второй кольцевой зоны, на расстоянии L+3λ/2 – гра­ницу третьей и т.д.

Обозначим Е₁ амплитуду волны, пришедшей в точку P от первой зоны, Е₂ – от второй и т.д. Колебания, приходящие в точку В от двух соседних зон, противоположны по фазе, так как их разность хода равна λ/2, они будут ослаблять друг друга. На­помним, что при прохождении волной пути в половину длины волны ее фаза меняется на противоположную. Поэтому при суммировании амплитуды нечетных зон будем брать со знаком «+», а четных – со знаком «-». В итоге результирующая ампли­туда, т.е. амплитуда колебаний от всех зон в точке P будет равна

Е = Е₁ – Е₂ + Е₃ – Е₄ +…+ Е_n.

С увеличением номера зоны амплитуда колебаний моно­тонно убывает, так как увеличивается расстояние от зоны до точки P и угол α между нормалью к поверхности зоны и на­прав­лением на точку наблюдения, поэтому по абсолютной вели­чине Е₁ > Е₂ > Е₃ > Е₄ >…> Е_n.

Из-за того, что число зон n очень велико (например, для λ= 500 нм и L = 10 см n = 80000), амплитуды двух соседних зон мало отличаются друг от друга по величине и с большой степе­нью точности можно предположить, что

. Если представить амплитуду любой не­четной зоны, например Е₁ как , то выражение для результирующей амплитуды запишется в виде

Согласно вышеприведенным рассуждениям все выраже­ния в скобках обращаются в нуль и Е ≈ Е₁/2. Результирующая амплитуда светового колебания от всей волновой поверхности в точке наблюдения равна половине амплитуды, приходящей от одной центральной зоны. Если на пути волны поставить непро­зрачный экран, оставляющий открытой только центральную зону Френеля, то амплитуда светового колебания в точке P бу­дет равняться Е₁, т.е. возрастет в два раза. Если экран открывает две зоны, их амплитуды будут «гасить» друг друга и в точке P будет наблюдаться минимум интенсивности. Если открыты три зоны, третья зона останется не скомпенсированной и в точке P будет наблюдаться максимум, и т.д. Таким образом, если на волновой поверхности открыто нечетное число зон Френеля, в точке наблюдения будет светло, если четное – темно. Если ме­жду волновой поверхностью и точкой P поставить специальную пластинку, которая закрывала бы все четные (или нечетные) зоны, то интенсивность в точке P резко возрастает. Такая пла­стинка называется зонной и действует подобно собирающей линзе.

Различают дифракцию Френеля – это дифракция в сходящихся или расходящихся лучах и дифракцию Фраунго­фера – в параллельных лучах. Разберем эти случаи более под­робно.