8. Первый закон термодинамики и его применение к различным процессам

Эквивалентность количества теплоты и механической работы была установлена в середине XIX в. английским ученым Джоулем и немецким ученым Майером. Это привело к открытию одного из самых фундаментальных законов физики — закона сохранения энергии: энергия не возникает из ничего и не исчезает; в различных процессах она только превращается из одного вида в другой в эквивалентных количествах.

Закон сохранения энергии в применении к тепловым процессам принято называть первым законом (или первым началом) термодинамики: внутренняя энергия системы может изменяться при совершении работы внешними силами над системой или в результате теплообмена: или количество теплоты, полученное системой, в общем случае расходуется на изменение ее внутренней энергии и на совершение системой работы против внешних сил:

.

1. Изобарный процесс. Работа газа.

П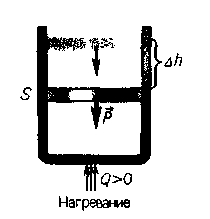 усть в цилиндре с незакрепленным невесомым поршнем находится идеальный газ (рис.). Нагреем его, сообщив газу количество теплоты Q. Поскольку поршень не закреплен, давление газа р постоянно и равно атмосферному. При нагревании на T происходит изобарное расширение газа и его объем увеличивается на V = Sh (где S - площадь поршня, h - высота поднятия поршня). Работа расширения газа А = Fh = pSh = рV.

Э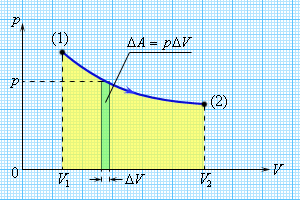 та формула для работы газа справедлива не только для изобарного процесса, но и для любого процесса, в котором объем газа изменяется на сколь угодно малую величину V.

При изобарном процессе количество теплоты, сообщаемое газу, расходуется как на его нагревание (т. е. на увеличение внутренней энергии), так и на работу расширения, которую газ совершает против сил внешнего давления. Поэтому первый закон термодинамики для изобарного процесса записывают в виде Q=A+U.

При изобарном нагревании газа на T его объем увеличивается на V. Работа газа при изобарном расширении может быть найдена как . В любом другом процессе работа газа может быть найдена как площадь под графиком процесса в р, V координатах. Из формулы для работы газа следует, что газовая постоянная численно равна работе которую совершает 1 моль идеального газа при изобарном нагревании на 1 К.

В результате для изобарного процесса можно записать:

.

Из этой записи следует, что молярная теплоемкость газа при постоянном давлении:

.

2. Изохорный процесс. Теорема Майера

Так как в данном процессе объем газа не изменяется, то V= 0, т.е. А = 0 - в изохорном процессе газ не совершает работы. Первый закон термодинамики принимает вид: Q = U - в изохорном процессе вся сообщаемая газу теплота идет на увеличение его внутренней энергии.

Для изохорного процесса можно записать:

.

Из этой записи следует, что молярная теплоемкость газа при постоянном объеме:

.

Теплоемкость газа зависит от вида процесса - теорема Майера (в честь немецкого врача, который одним из первых сформулировал закон сохранения и превращения энергии применительно к тепловым процессам): молярная теплоемкость идеального газа при постоянном давлении равна сумме молярной теплоемкости этого газа при постоянном объеме и молярной газовой постоянной.

Молярная теплоемкость идеального газа при постоянном давлении или при постоянном объеме не зависит от его химического состава и температуры, а зависит только от числа степеней свободы молекул, которое в свою очередь зависит от числа атомов в этих молекулах.