6. Основное уравнение молекулярно-кинетической теории идеального газа

О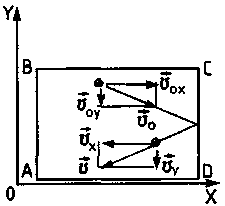 сновное уравнение молекулярно-кинетической теории идеального газа устанавливает зависимость между макро и микро параметрами.

Вычислим давление газа на стенку CD сосуда ABCD площадью S, перпендикулярную координатной оси Ох.

Каждая молекула массой m₀, подлетающая к стенке сосуда со скоростью , проекция которой на ось Ох равна _x, передает стенке при ударе импульс m₀_x. Отскакивая от стенки с той же по модулю скоростью, молекула опять передает стенке импульс m₀_x. Всего за время столкновения молекула передает стенке импульс 2 m₀_x. Молекул много, и каждая из них передает стенке при столкновении такой же импульс. (Все молекулы при одной и той же температуре имеют разные скорости, поэтому говоря о скорости молекулы подразумеваем среднюю квадратичную скорость). За время t они передадут стенке импульс 2m₀_xZ, где Z — число столкновений всех молекул со стенкой за это время. Число Z, прямо пропорционально концентрации молекул, числу молекул в единице объема . Кроме того, число Z пропорционально скорости молекул _x. Чем больше эта скорость, тем больше молекул за время t успеет столкнуться со стенкой. Кроме того, число столкновений молекул со стенкой пропорционально площади поверхности стенки S. Надо еще учесть, что в среднем только половина всех молекул движется к стенке. Другая половина движется в обратную сторону. Поэтому . Полный импульс, переданный стенке за 1 с, равен: . Согласно второму закону Ньютона изменение импульса любого тела за единицу времени равнодействующей на него силе: . Т.к. и . Таким образом, давление газа на стенку сосуда равно: - основное уравнение молекулярно-кинетической теории. Формула связывает макроскопическую величину — давление, которое может быть измерено манометром, — с микроскопическими величинами, характеризующими молекулы.

Основное уравнение МКТ может быть записано в виде:

Последняя формула получена экспериментально. Сравнивая два последних выражения получаем связь между средней кинетической энергией поступательного движения молекул и температурой.

. Здесь - постоянная Больцмана.

Следует учесть, что .

Физический смысл постоянной Больцмана состоит в том, что она выражает связь между значением температуры, выраженной в Кельвинах, и тем же значением температуры, выраженной в энергетических единицах, т. е устанавливает непосредственную связь между джоулем и Кельвином.

Число Лошмидта

При одинаковых давлениях и температурах концентрация молекул всех газов одинакова. В частности, при нормальных условиях - число Лошмидта, оно равно количеству молекул идеального газа, содержащихся в 1 м³ газа при нормальных условиях.

Закон Дальтона для парциальных давлений в газовой смеси

Парциальным называют такое давление газа, входящего в состав газовой смеси, которое этот газ производил бы на стенки камеры, если бы только он один занимал весь объем, заполненный газовой смесью.

Т. к. концентрация молекул газовой смеси равна сумме концентраций молекул всех газов, входящих в состав этой смеси, то давление в газовой смеси равно сумме парциальных давлений всех газов, входящих в эту смесь.