7. Центростремительное ускорение (вывод формулы).

Равномерное движение тела по окружности является движением с ускорением. Ускорение направлено по радиусу к центру окружности. Его называют нормальным или центростремительным ускорением. Модуль центростремительного ускорения связан с линейной  υ  и угловой ω скоростями соотношениями: 

Д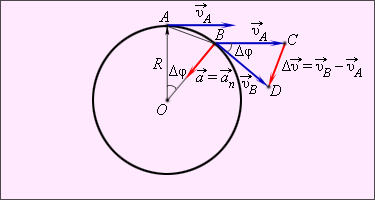 ля доказательства этого выражения рассмотрим изменение вектора скорости за малый промежуток времени Δt. По определению ускорения

Векторы скоростей и в точках A и B направлены по касательным к окружности в этих точках. Модули скоростей одинаковы υ_A = υ_B = υ.

Из подобия треугольников OAB и BCD (рис.) следует: .

При малых значениях угла Δφ = ωΔt  расстояние |AB| =Δs ≈ υΔt. Так как |OA| = R и |CD| = Δυ, из подобия треугольников на рис.  получаем:  .

При малых углах Δφ направление вектора  приближается к направлению на центр окружности. Следовательно, переходя к пределу при Δt → 0. При изменении положения тела на окружности изменяется направление на центр окружности. При равномерном движении тела по окружности модуль ускорения остается неизменным, но направление вектора ускорения изменяется со временем. Вектор ускорения в любой точке окружности направлен к ее центру. Поэтому ускорение при равномерном движении тела по окружности называется центростремительным.

Центростремительное ускорение показывает как быстро изменяется направление скорости. Любое криволинейное движение – это движение с ускорением.

9. Закон сохранения импульса (вывод, границы применения)

Физическая величина, равная произведению массы тела на скорость его движения, называется импульсом тела (или количеством движения). Импульс тела – векторная величина. . Единицей измерения импульса в СИ является килограмм-метр в секунду (кг·м/с).

Физическая величина, равная произведению силы на время ее действия, называется импульсом силы . Импульс силы также является векторной величиной.

В новых терминах второй закон Ньютона может быть сформулирован следующим образом: изменение импульса тела (количества движения) равно импульсу силы

Именно в таком общем виде сформулировал второй закон сам Ньютон. Сила в этом выражении представляет собой равнодействующую всех сил, приложенных к телу. Это векторное равенство может быть записано в проекциях на координатные оси, например F_x Δt = Δp_x. Таким образом, изменение проекции импульса тела на любую из трех взаимно перпендикулярных осей равно проекции импульса силы на эту же ось. При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу.

Если на систему тел не действуют внешние силы со стороны других тел, то такая система называется замкнутой. Импульс системы тел равен векторной сумме импульсов тел, составляющих эту систему:

В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.

Этот фундаментальный закон природы называется законом сохранения импульса. Он является следствием из второго и третьего законов Ньютона.

Р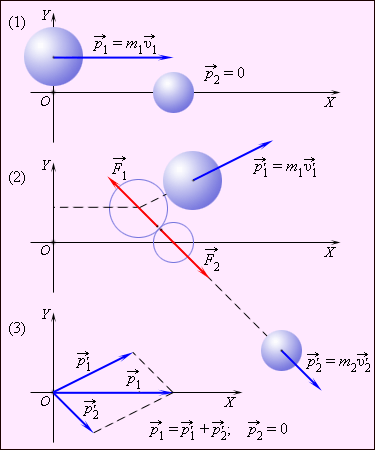 ассмотрим какие-либо два взаимодействующих тела, входящих в состав замкнутой системы. Силы взаимодействия между этими телами обозначим через и . По третьему закону Ньютона если эти тела взаимодействуют в течение времени t, то импульсы сил взаимодействия одинаковы по модулю и направлены в противоположные стороны: . Применим к этим телам второй закон Ньютона: и , где и – импульсы тел в начальный момент времени, и – импульсы тел в конце взаимодействия. Из этих соотношений следует:

.

Это равенство означает, что в результате взаимодействия двух тел их суммарный импульс не изменился. Рассматривая теперь всевозможные парные взаимодействия тел, входящих в замкнутую систему, можно сделать вывод, что внутренние силы замкнутой системы не могут изменить ее суммарный импульс, т. е. векторную сумму импульсов всех тел, входящих в эту систему.

Закон сохранения импульса выполняется и для проекций векторов на каждую ось.

Примером может служить реактивное движение. При стрельбе из орудия возникает отдача – снаряд движется вперед, а орудие – откатывается назад. Снаряд и орудие – два взаимодействующих тела.

На принципе отдачи основано реактивное движение. В ракете при сгорании топлива газы, нагретые до высокой температуры, выбрасываются из сопла с большой скоростью  относительно ракеты.

Закон сохранения импульса можно применять для всех быстро протекающих процессов: столкновения, удар, взрыв – когда время взаимодействия тел мало.