15. Необратимость тепловых процессов. Второй закон термодинамики и его статистический смысл

В термодинамике любую группу тел или частиц называют термодинамической системой. Если на термодинамическую систему не действуют внешние силы, то она самопроизвольно переходит в состояние теплового равновесия — состояние, при котором все ее термодинамические параметры: давление, объем, температура с течением времени будут оставаться постоянными. При выводе термодинамической системы из равновесного состояния вследствие изменения одного или нескольких параметров она станет переходить через ряд промежуточных состояний, пока не перейдет в новое состояние с новыми параметрами, Такой переход называется термодинамическим процессом. Если термодинамическая система, претерпев ряд изменений, возвращается в исходное состояние с первоначальными параметрами, то такой процесс называется круговым (или замкнутым, или циклом). Самопроизвольным называется такой процесс, при котором в телах, окружающих термодинамическую систему, не происходит никаких изменений. Иными словами, самопроизвольный процесс - процесс, который протекает в термодинамической системе без внешнего воздействия. Обратимым называется процесс, который может самопроизвольно протекать как в прямом, так и в обратном направлениях. Термодинамические процессы, которые не могут протекать самопроизвольно как в прямом, так и в обратном направлениях, называются необратимыми (например, расширение газа).

Событие, вероятность которого равна нулю, невероятно, т. е. невозможно. Например, все молекулы газа сами никогда не смогут одновременно оказаться в одной половине сосуда, т. е. газ самопроизвольно сжаться не может. По той же причине тепло не может самопроизвольно перейти от холодного тела к горячему, такой процесс невероятен, хотя прямой переход тепла от горячего тела к холодному реален. При трении прямой процесс перехода механической энергии во внутреннюю возможен, а обратный нет.

Любые термодинамические процессы со статистически огромным количеством молекул и атомов могут самопроизвольно протекать только в одном направлении, т. е. они необратимы, поскольку вероятность обратного процесса равна нулю. Это утверждение называется вторым законом (вторым началом) термодинамики. Вот некоторые другие его формулировки.

Второй закон термодинамики:

а) любые самопроизвольные процессы в термодинамической системе, состоящей из статистически огромного числа частиц, всегда переводят эту систему из менее вероятного состояния в более вероятное и никогда наоборот;

б) невозможен самопроизвольный процесс передачи тепла от тел, менее нагретых, телам, более нагретым;

в) невозможно изготовить вечный двигатель второго рода - устройство, в котором бы все тепло, полученное от нагревателя, полностью превращалось бы в механическую работу.

В этом состоит статистический смысл второго закона термодинамики.

Механика

1. Аналитическое описание равноускоренного движения. Вывод формул для перемещения при равноускоренном движении

В общем случае равноускоренным движением называют такое движение, при котором вектор ускорения остается неизменным по модулю и направлению. Примером такого движения является движение камня, брошенного под некоторым углом к горизонту (без учета сопротивления воздуха). В любой точке траектории ускорение камня равно ускорению свободного падения . Таким образом, изучение равноускоренного движения сводится к изучению прямолинейного равноускоренного движения. В случае прямолинейного движения векторы скорости и ускорения направлены вдоль прямой движения. Поэтому скорость и ускорение в проекциях на направление движения можно рассматривать как алгебраические величины. При равноускоренном прямолинейном движении скорость тела определяется формулой (1)

В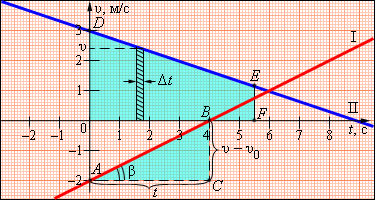 этой формуле – скорость тела при t = 0 (начальная скорость),   = const – ускорение. В проекции на выбранную ось х уравнение (1) запишется в виде: (2). На графике проекции скорости υ_х(t) эта зависимость имеет вид прямой линии.

По наклону графика скорости может быть определено ускорение a тела. Соответствующие построения выполнены на рис. для графика I Ускорение численно равно отношению сторон треугольника ABC: .

Чем больше угол β, который образует график скорости с осью времени, т. е. чем больше наклон графика (крутизна), тем больше ускорение тела.

Для графика I: υ₀ = –2 м/с, a = 1/2 м/с². Для графика II: υ₀ = 3 м/с, a = –1/3 м/с².

График скорости позволяет также определить проекцию перемещения s тела за некоторое время t. Выделим на оси времени некоторый малый промежуток времени Δt. Если этот промежуток времени достаточно мал, то и изменение скорости за этот промежуток невелико, то есть движение в течение этого промежутка времени можно считать равномерным с некоторой средней скоростью, которая равна мгновенной скорости υ тела в середине промежутка Δt. Следовательно, перемещение Δs за время Δt будет равно Δs = υΔt. Это перемещение равно площади заштрихованной на рис. полоски. Разбив промежуток времени от 0 до некоторого момента t на малые промежутки Δt, можно получить, что перемещение s за заданное время t при равноускоренном прямолинейном движении равно площади трапеции ODEF. Соответствующие построения выполнены на рис. для графика II. Время t принято равным 5,5 с.

(3) – полученная формула позволяет определить перемещение при равноускоренном движении если ускорение не известно.

Если подставить в уравнение (3) выражение для скорости (2), то получаем (4) – эта формула используется для записи уравнения движения тела: (5).

Если выразить из уравнения (2) время движения (6) и подставить в равенство (3), то

- эта формула позволяет определить перемещение при неизвестном времени движения.