Статические преобразователи частоты

Схема преобразования с непосредственной связью

В основе схемы трех фазное выпрямление состоящее из двух частей:

1. 3 теристора объединенных общем катодом, выпрямительная группа.

2. 3 теристора объединенных общим анодом, инверторная группа.

Управление преобразователем может осуществляться по разным схемам либо по совместной схеме.

Совместная – от одного источника питания.

Раздельная - от других источников питания.

Что бы исключить к.з. управляющие импульсы должны подаваться на теристоры одной группы в соответствии с направлением протекающим по ним токам нагрузки, что бы обеспечить работу схемы управления используют в ней логические элементы.

Получение различной величины выходного напряжения зависит от  - угла регулирования теристоров.

+ Высокий КПД; свободный обмен активной, реактивной энергии от сети к двигателю и обратно; отсутствие коммутационной аппаратуры; незначительные потери энергии.

- Ограниченное регулирование выходной частоты, от 0% до 40% частоты сети; большое число теристоров, что усложняет схему управления; относительно невысокий cos=0,7

Применение: в высокочастотных сетях, используется в тихоходных безредукторных приводах, особенно для механизмов больших объемов и производительности.

Кроме вышеперечисленных существуют:

• Статические преобразователи частоты с промежуточным звеном постоянного I (позволяет регулировать частоту как вверх так и вниз от основной, имеет высокий КПД, быстродействие, малые габариты, повышенную надежность).

• Статические преобразователи частоты переменного током с промежуточным звеном (позволяющие получать трех фазное напряжение из однофазного, но в результате получаются большие пульсации выпрямленного напряжения).

(конспект для самостоятельного изучения)

Тема: Основы электропривода

3 Динамика электропривода. Расчет мощности и выбор электропривода

1.Динамика электрических приводов и переходные процессы

2.Тепловой режим электродвигателей.

3.Режимы работы электродвигателей и определение их необходимой мощности.

Литература.

3. Онищенко г.Б. Электрический привод. – м.: Академия. 2008 г., §§ 8, 10.2-10.3, 11.3-11.4

4. Москаленко В.В. Электрический привод. – М.: Академия. 2007 г. Гл. 8,9

Динамика электрических приводов и переходные процессы

Основное уравнение движения

J – момент инерции, мера инерционности масс при вращательном движении.

Момент инерции тела относительно оси вращения это масса некоторого тела расположенного в материальной точке (центр тяжести) на расстоянии р от оси вращения.

Для симметричных тел вращения J можно посчитать аналитически

Для несимметричных тел опытным путем.

Мд – момент двигателя

Мс – момент сопротивления рабочей машины.

подставляется в формулу приведенным к скорости одного вала.

 необходимо определение приведение их приведенных величин.

Приведение момента двигателя и сопротивления к скорости вала.

Скорость вала к которой приводится момент и сила выбирается расчетом по его усмотрению.

Моментом сопротивления приведенной к скорости данного вала называется момент создаваемый на данном валу тем моментом, который создается приводом к данной скорости

Mc` - приведенный момент (момент создаваемой рабочей машиной на валу двигателя

- отношение передаточного числа

Если расчет ведется относительно вала машины то Mд`=Mд I * n_пер (расчитывается приведенный момент движения

Приведение момента инерции и поступательного движения масс, к скорости вала.

В процессе работы вращательного и поступательного движения запасают кинетическую энергию пропорционально квадрату соответствующих скоростей и величины масс.

При всяком изменении скорости (ускорения) появляются динамические моменты обусловленные изменением запаса кинетической энергии

;

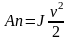
Запас кинетической энергии вращающейся части; Запас кинетической энергии поступательной части

Приведенной к скорости данного вала моментом инерции называется момент инерции некоторого условного маховика, который вращается со скоростью данного вала способен запасать кинетическую энергию равной суммы кинетической энергии запасаемую всеми подвижными частями.

Разделим это выражение на

Определение приведенных моментов инерции деталей и агрегатов

Jвр=m*p²; p- радиус инерции

Д ля симметричной детали p=R²/2

П олый цилиндр p=(R²+ R²)/2

Д еталь прямоугольной формы p²=(a²+b²)/12

Если трудно вычислить момент инерции, проводят эксперимент (методом математического маятника). Для этого взвешивают агрегат (барабан). Измеряют а (расстояние между системой), l (высота подвеса) и определяют время крутильных колебаний, закручивают деталь на определенный угол и отпускают ее измеряют время 10 полных колебаний и первого колебания. Вычисляют момент инерции по формуле:

При весе подвески много меньшей детали Pп<<Рб

Рб – вес барабана

Рп – вес подвески

Тб – время колебания барабана

g – ускорение свободного падения