Примеры выполнения заданий.

Задание 1. Произведено по 4 испытания на каждом из трех уровней. Результаты испытаний приведены в таблице 4. Методом дисперсионного анализа на уровне значимости 0,05 проверить нулевую гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.

Таблица 4.

Номер испытания	Уровни фактора Fj
	F1	F2	F3
1	51	52	42
2	52	54	44
3	56	56	50
4	57	58	52
Групповое среднее	54	55	47

Решение. Для упрощения расчетов вычтем с=52 из каждого наблюдаемого значения: y_ij=x_ij-52 ( ).

1). Сформулируем нулевую гипотезу H₀ и альтернативную H₁:

H₀: ₁ = ₂ = ₃; H₁: «По крайней мере 2_j (j = 1, 2, 3) различны”.

2). α = 0,05.

3). Составим расчетную таблицу 5. Пользуясь таблицей и учитывая, что число уровней р=3, а число испытаний на каждом уровне q=4, найдем факторную и остаточную суммы квадратов отклонений.

Таблица 5

Номер испытания	Уровни фактора Fj						Итоговый столбец
	F1		F2		F3
	yi1	yi12	yi2	yi22	yi3	yi32
1	-1	1	0	0	-10	100
2	0	0	2	4	-8	64
3	4	16	4	16	-2	4
4	5	25	6	36	0	0
		42		56		168
	8		12		-20
	64		144		400

В соответствии с обозначениями таблицы перепишем формулы для вычисления факторной и остаточной дисперсий:

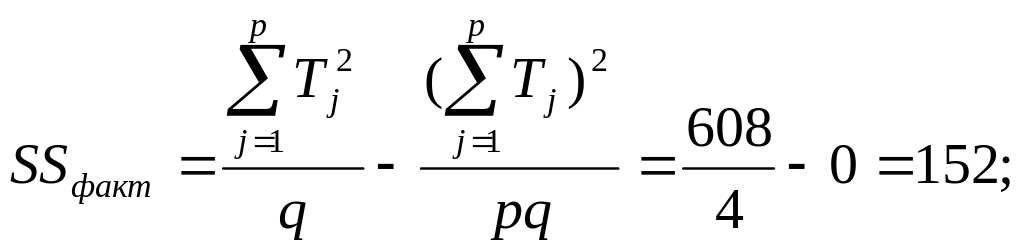
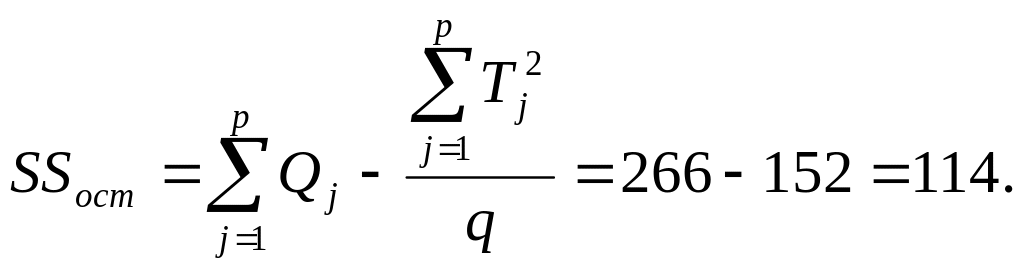
Найдем факторную и остаточную дисперсии:

4). Сравним факторную и остаточную дисперсии по критерию Фишера-Снедекора, для чего найдем наблюдаемое значение критерия:

Учитывая, что число степеней свободы числителя k₁=2, а знаменателя k₂=9 и уровень значимости α=0,05, по таблице критических точек распределения Фишера-Снедекора находим критическую точку:

F_кр(0,05; 2; 9)=4,26.

Так как 6 > 4,26, т. е. F_набл > F_кр , то нулевая гипотеза о равенстве групповых средних отвергается, а значит групповые средние различаются значимо. Если требуется сравнить средние попарно, то следует воспользоваться критерием Стьюдента.

Лабораторная работа № 3.

Тема: Факторный анализ: метод главных компонент.

Теоретическая часть.

Реализация метода главных компонент (МГК) на ЭВМ наиболее полно и грамотно проведена в рамках возможностей программы статистического анализа ТSP. TSP – это профессиональная программная система и эконометрический язык с большим количеством статических возможностей. Для выполнения МГК в программе TSP используется оператор PRIN.

Назначение оператора PRIN: реализует МГК для нескольких переменных; количество главных компонент может быть фиксировано или определяться в процессе анализа. Исходные данные для этого оператора должны быть организованы в виде матрицы «объект – свойство», столбцы которой представляют собой значения анализируемых переменных на заданных объектах.

Синтаксис оператора PRIN:

PRIN (NCOM=<количество главных компонент>, FRAC=<доля дисперсии>) <список переменных>;

где NCOM – максимальное количество главных компонент, получаемых на выходе МГК, реальное количество главных компонент определяется минимумом из NCOM и количества главных компонент, описывающих значение FRAC;

FRAC – доля дисперсии входных переменных, которую должны описывать главные компоненты, в теории обозначается буквой γ (это вероятностная характеристика, поэтому она не должна превышать 1).

Результат работы оператора PRIN: вывод результата начинается с заголовка, списка входных переменных, количества наблюдений и корреляционной матрицы исходных переменных. Далее следует вывод таблицы главных компонент, в которой для каждой главной компоненты, имя которой начинается с буквы Р, печатается ее значение и суммарный вклад в общую дисперсию. Затем выводится таблица весовых коэффициентов главных компонент. Эти весовые коэффициенты являются коэффициентами корреляции между исходными переменными и главными компонентами и показывают степень линейной связи между ними.

Матрица весовых коэффициентов А в итоговом отчете программы TSP выводится в виде таблицы: столбцы весовых коэффициентов соответствуют выбранным главным компонентам, элементы столбцов соответствуют исходным переменным.

Замечания: 1). ТSP преобразует исходные данные в стандартизированные.

2). TSP создан для обработки данных, изменяющихся во времени. Поэтому для указания количества объектов нужно задать частоту наблюдений ежегодно (FREQ A;) и количество наблюдений с помощью оператора SMPL (например, SMPL 2001 2020; для 20 объектов).

3). Исходные данные в виде матрицы «объект-свойство» должны представлять собой текстовый файл. Для загрузки исходных данных в переменные используется оператор LOAD.

Пример. Исходные данные и строка команды оператора PRIN.

FREQ A;

SMPL 1901 1905 ;

LOAD X1 X2 X3 X4 ;

0.818 0.455 0.591 0.545

0.273 0.545 0.773 0.182

0.091 0.682 0.591 0.227

0.727 0.636 0.682 0.409

0.455 0.682 0.227 0.636 ;

PRIN(FRAC=0.9) X1 X2 X3 X4 ;

Результат обработки данных методом главных компонент с помощью пакета TSP.

TSP Version 4.3A

PROGRAM

Current sample: 1901 to 1905

PRINCIPAL COMPONENTS

====================

VARIABLES: X1 X2 X3 X4

Number of Observations: 5

Correlation Matrix(корреляционная матрица)

X1 X2 X3 X4

X1 1.00000

X2 -0.52333 1.0000

X3 -0.026754 -0.44752 1.0000

X4 0.66050 -0.045826 -0.76551 1.00000

Название и значение главных компонент, а также их вклад в общую дисперсию.

Component Name Eigenvalue Cumulative R-Squared

1 P1 2.0266668 0.50666669

2 P2 1.6737097 0.92509412

Таблица весовых коэффициентов.

Factor Loadings

P1 P2

X1 0.70637 0.63238

X2 -0.089158 -0.91995

X3 -0.72369 0.65130

X4 0.99802 -0.057491