Часть 3. Решение.

1. Определяем среднее арифметическое и стандартное отклонение для данных таблицы 5:

(3.1)

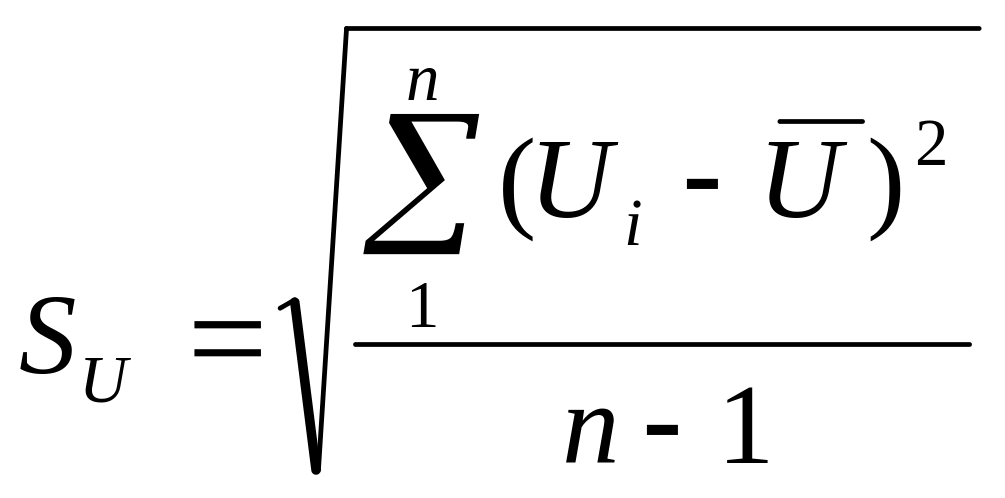(3.2)

2. С помощью правила «трех сигм» проверяем наличие или отсутствие промахов.

Таким образом, ни один из результатов не выходит за границы интервала , следовательно, с вероятностью 0,9973 гипотеза об отсутствии грубых погрешностей принимается.

3. Построение гистограммы и выдвижение гипотезы о виде закона распределения вероятности.

Для этого разбиваем вариационный ряд значений напряжения (таблица 1) на 11 интервалов.

Рассчитываем значение интервалов по формуле (3.3).

, (3.3)

где k – число интервалов .

Примем k=10

.

Выбираем начало первого интервала равным

Конец последнего (10 интервала) в точке

Затем для каждого интервала подсчитывается количество результатов , попавших в данный интервал и определяется

(3.4)

Результаты производимых вычислений заносятся в таблицу 6.

Таблица 6.

№	Uj-1	Uj	mj	zj	Ф(zj)	Pj	mj-nPj	Χ²j
1	-	33,21291	0	-	0	0,006	-0,6	0,6
2	33,21291	33,33446	2	-2,24998	0,0123	0,0063	1,37	2,979206
3	33,33446	33,45601	4	-1,49996	0,0668	0,0545	-1,45	0,38578
4	33,45601	33,57756	18	-0,74995	0,22662	0,15982	-1,982	0,245797
5	33,57756	33,69911	28	6,17E-05	0,5	0,27338	4,662	0,79502
6	33,69911	33,82066	24	0,750074	0,7734	0,2734	-3,34	0,408032
7	33,82066	33,94221	17	1,500086	0,9332	0,1598	1,02	0,065106
8	33,94221	34,06376	6	2,250099	0,9877	0,0545	0,55	0,055505
9	34,06376	34,18531	1	3,000111	0,9986	0,0109	-0,09	0,007431
10	34,18531	-	0	-	1	0,0014	-0,14	0,14

Затем строится гистограмма (рис.1). При построении гистограммы выбираем масштаб таким образом, чтобы высота относилась к основанию как 5 к 8.

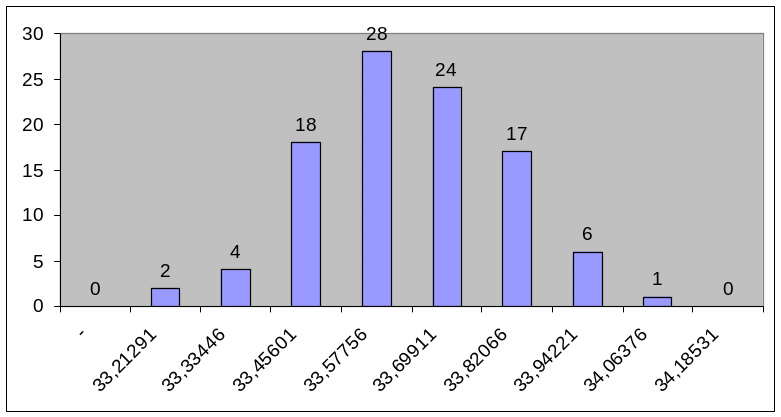
Рис. 1 Гистограмма

Из вида гистограммы на рис 1 можно сделать предположение о том, что вероятность результата измерения подчиняется нормальному закону. Проверим правдивость этой гипотезы.

4. Проверка нормальности закона распределения по критерию Пирсона.

Если выдвинута гипотеза о нормальности распределения, то для расчета вероятностей используется функция Лапласа по формуле (3.5)

,(3.5)

где значения и соответствуют началу и концу интервала соответственно. При этом учитываем, что конец предыдущего интервала является началом следующего интервала. Для каждого из этих значений рассчитаем относительный доверительный интервал по формуле (3.6)

,(3.6)

а затем из таблиц функции Лапласа найдем соответственные значения и

. Данные заносим в таблицу 2.

Находим доверительную вероятность для каждого интервала по формуле (3.7).

(3.7)

Затем рассчитаем значение и найдем суммарное значение

Данные расчета занесем в таблицу 2.

Определим табличное (критическое) значение , задавшись доверительной вероятностно 0,92 и вычислив по формуле r = k - 3 число степеней свободы:

.

.

Таким образом, с вероятностью 0,92 гипотеза о нормальности распределения вероят­ности результата измерения напряжения принимается.

5. В тех же координатах, что и гистограмма, строим теоретическую кри­вую плотности вероятности. Для этого рассчитываем значения плотности вероятности для середины каждого интервала . Результат расчета заносим в таблицу 2. Эти значения откладываем как ординаты из середин соответ­ствующих интервалов; полученные точки соединяем плавной кривой, симметричной отно­сительно математического ожидания (среднего арифметического значения) (рис.1).

6. Представление результата в виде доверительного интервала.

Для этого определим стандартное отклонение среднего арифметического по формуле (3.8):

,(3.8)

.

Закон распределения вероятности для среднего арифме­тического считаем нормальным (что следует из нормальности распределения самой изме­ряемой величины), тогда доверительный интервал определяем по выражению , при до­верительной вероятности 0,92. Этому значению соответствует аргумент функции Лаплапса t = 1,771.

Так как закон распределения вероятности для среднего арифметического счи­тается неизвестным, то относительный доверительный интервал рассчитываем в соответст­вии с неравенством Чебышева (3.9):

(3.9)

,

Как видно из сравнения результатов, неизвестность закона распределения вероятно­сти приводит к расширению доверительного интервала, то есть к увеличению дефицита из­мерительной информации.