
- •Дослід, якісна та кількісна характеристика досліду. Неможлива та достовірна події.Протилежна подія.
- •Сума, добуток, різниця подій. Несумісні події. Повна група несумісних подій.
- •Частота та відносна частота події. Властивості відносних частот.
- •Статистична ймовірність події. Аксіоми теорії ймовірностей. Вимірювання ймовірності на практиці.
- •Властивості ймовірностей.
- •Умовна відносна частота. Відносна частота добутку подій. Умовна ймовірність події. Формула множення ймовірностей та формула для умовної ймовірності.
- •Залежні та незалежні події. Теорема множення для незалежних подій.
- •Простий дослід. Класичне означення ймовірностї. Геометричні ймовірності.
- •Формули комбінаторики.
- •Формула повної ймовірності та формула Байєса.
- •Повторні випробування та формула Бернуллі.
- •Наближені формули до формули Бернуллі.
- •Випадкова величина. Функція розподілу та її властивості.
- •Дискретна випадкова величина. Закон розподілу, полігон, функція розподілу.
- •Абсолютно неперервна випадкова величина, її функція розподілу та щільність розподілу. Властивості щільності.
- •Математичне сподівання випадкової величини та його властивості.
- •Властивості математичного сподівання
- •Дисперсія випадкової величини та її властивості.
- •Властивості дисперсії
- •Моменти, асиметрія, ексцес. Мода, медіана та квантилі.
- •Рівномірний розподіл.
- •Стандартний нормальний розподіл.
- •Нормальний розподіл та його властивості. Центральна гранична теорема.
- •Властивості нормальних розподілів
- •Центральна гранична теорема Ляпунова
- •Показниковий розподіл, його властивості.
- •Біноміальний розподіл.
- •Розподіл Пуассона. Потоки найпростіших подій.
- •Геометричний та гіпергеометричний розподіли. Розподіл Пірсона.
- •Розподіл - Пірсона
- •Нерівність Маркова та Чебишова.
- •Теореми Хінчина, Чебишова та Бернуллі.
- •Двовимірна випадкова величина. Основні означення.
- •Числові характеристики двовимірної випадкової величини.
- •Означення регресії. Теорема про лінійну регресію. Властивості коефіцієнта кореляції.
- •Властивості коефіцієнта кореляції
- •Умовне математичне сподівання та його властивості.
- •Властивості mxy
- •Теорема про умовне математичне сподівання. Властивості кореляційного відношення.
- •Властивості кореляційного відношення
- •Двовимірний нормальний розподіл та його властивості.
- •Означення вибірки, статистики, оцінки параметра, міри розсіювання параметра. Теорема про міру розсіювання.
- •Означення незміщеної, асимптотично незміщеної, конзистентної та ефективної оцінок. Оцінки
- •Оцінка дисперсії. Виправлена дисперсія. Їх властивості.
- •Емпірична функція розподілу. Емпіричний розподіл. Кумулята, полігон, гістограма.
- •Емпіричні оцінки параметрів розподілу та їх властивість.
- •Метод моментів для побудови оцінок.
- •Метод найбільшої правдоподібності.
- •Надійний інтервал. Його побудова, якщо відомий розподіл оцінки параметра.
- •Надійні інтервали для параметрів з стандартно нормально розподіленими оцінками.
- •Надійні інтервали для параметрів нормального розподілу.
- •Асимптотично нормальні оцінки. Приклади та їх надійні інтервали.
- •Поняття критерію згоди. Критерій згоди Пірсона.
- •Перевірка гіпотез з допомогою надійних інтервалів. Метод найменших квадратів.
Числові характеристики двовимірної випадкової величини.
Математичне сподівання двовимірної випадкової величини – це числовий вектор, який складається з математичних сподівань Х і Y: M(X,Y)=(MX, MY).
Відхилення
випадкової величини (X,Y)
– це випадкова величина (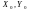 ),
де
),
де
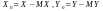 – відхилення випадкових величин X та Y
відповідно. Можна, згадавши додавання
векторів, ще й так записати:
(
)=(X-MX,Y-MY)=(X,Y)-(MX,
MY)=(X,Y)-M(X,Y).
– відхилення випадкових величин X та Y
відповідно. Можна, згадавши додавання
векторів, ще й так записати:
(
)=(X-MX,Y-MY)=(X,Y)-(MX,
MY)=(X,Y)-M(X,Y).
Кореляційна матриця двовимірного розподілу це числова матриця
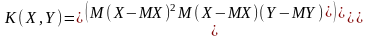 =
=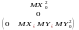
Коваріація
– це число
сov(X,Y)=cov=M(X-MX)(Y-MY)=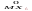 .
.
Є зручна в деяких випадках формула для коваріації аналогічна другій формулі для дисперсії:
сov(X,Y)=MXY-MX MY.
Доведення. cov=M(XY)-M(XMY)-M(YMX)+MXMY=MXY-MXMY.
Отже,
кореляційна матриця: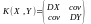 .
.
Коефіцієнт
кореляції це число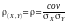 .
.
Інші
формули для коефіцієнта кореляції:
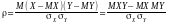 .
.
Означення регресії. Теорема про лінійну регресію. Властивості коефіцієнта кореляції.
Можна розглядати
різні функції від випадкової величини
Х і пробувати наближати ними в.в. Y:
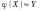 .
Величина
.
Величина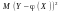 називається похибкою наближення
називається похибкою наближення
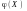 .Функція
називається найкращим наближенням Y
через Х (регресією Y на Х), якщо її
похибка наближення
найменша
з похибок всіх функцій.
.Функція
називається найкращим наближенням Y
через Х (регресією Y на Х), якщо її
похибка наближення
найменша
з похибок всіх функцій.
Найкраще наближення серед лінійних функцій називається лінійною регресією Y на Х .
Теорема. Лінійна регресія
Y на Х це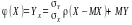 .
ЇЇ похибка дорівнює
.
ЇЇ похибка дорівнює
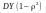 .
.
Властивості коефіцієнта кореляції
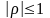 (наслідок теореми, бо похибка наближення
невід'ємна).
(наслідок теореми, бо похибка наближення
невід'ємна).Якщо X, Y незалежні, то
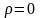 ,
але навпаки при
,
але навпаки при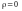 розподіли
Х, Y не обов'язково незалежні, а можуть
бути тільки некорельованими
розподіли
Х, Y не обов'язково незалежні, а можуть
бути тільки некорельованими
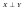 .
.
Якщо
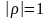 ,
то Y є лінійною функцією
від Х (наслідок теореми, тоді похибка
буде нулем), тобто Y = aX +
b (точніше Р(Y = aX + b) =1).
,
то Y є лінійною функцією
від Х (наслідок теореми, тоді похибка
буде нулем), тобто Y = aX +
b (точніше Р(Y = aX + b) =1).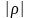 характеризує тісноту лінійної залежності,
якщо
характеризує тісноту лінійної залежності,
якщо
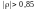 ,
то кажуть сильна лінійна залежність,
якщо
,
то кажуть сильна лінійна залежність,
якщо
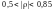 - середня, якщо
- середня, якщо
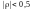 - слабка.
- слабка.Якщо
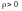 ,
то пряма лінійна залежність (при
зростанні X зростає в середньому й Y).
Якщо
,
то пряма лінійна залежність (при
зростанні X зростає в середньому й Y).
Якщо
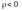 – непряма лінійна залежність (при
зростанні X в середньому спадає Y).
– непряма лінійна залежність (при
зростанні X в середньому спадає Y).
Умовне математичне сподівання та його властивості.
Для
дискретного сумісного розподілу (X,Y)
умовне математичне сподівання Y відносно
X позначають MХY
– функція від розподілу Х (
),
яка кожному можливому значенню
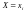 ставить у відповідність (прогнозує для
в.в.Y) середнє значення з усіх можливих
значень в.в.Y при умові, що вже сталась
подія
,
яке позначається
ставить у відповідність (прогнозує для
в.в.Y) середнє значення з усіх можливих
значень в.в.Y при умові, що вже сталась
подія
,
яке позначається
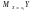 .
.
Властивості mxy
М(MХY)= MY.
Доведення.
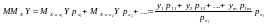 +
+
+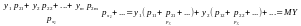 .
.
2. Якщо X, Y - незалежні випадкові величини, то MXY = MY – стала випадкова величина.
3.
Якщо Y є
функцією від Х (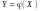 ),
то MХY=
=Y,
тобто умовне мат. сподівання якраз буде
цією функцією, буде найкращим наближенням.
Маємо формулу
),
то MХY=
=Y,
тобто умовне мат. сподівання якраз буде
цією функцією, буде найкращим наближенням.
Маємо формулу
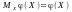 -- подібна на формулу математичного
сподівання сталої.
-- подібна на формулу математичного
сподівання сталої.
Теорема про умовне математичне сподівання. Властивості кореляційного відношення.
Теорема 2.
Найкращим наближенням Y
через X(регресією Y
на X) є умовне мат. сподівання
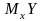 .
.
Властивості кореляційного відношення
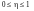 (
наслідок теореми 2).
(
наслідок теореми 2).Якщо X, Y – незалежні, то
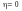 .
.Якщо , то розподіл Y- кореляційно незалежний від розподілу Х.
Доведення. Якщо X і Y незалежні, то за другою властивістю MХY стала, а для сталої дисперсія дорівнює нулю.
Якщо
,
то
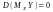
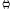 MХY-
стала, тобто, значення випадкової
величини X не впливають на середнє
значення випадкової величини Y.
MХY-
стала, тобто, значення випадкової
величини X не впливають на середнє
значення випадкової величини Y.
Y є функцією Х, тоді і тільки тоді, коли
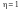 ,
оскільки лише тоді похибка наближення
буде дорівнювати 0. Отже,
,
оскільки лише тоді похибка наближення
буде дорівнювати 0. Отже,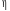 характеризує ступінь залежності Y та
X. Чим ближче
до 1, тим сильніша залежність.
характеризує ступінь залежності Y та
X. Чим ближче
до 1, тим сильніша залежність.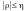 тому,
що похибка лінійного наближення не
менша, ніж похибка найкращого з наближень:
тому,
що похибка лінійного наближення не
менша, ніж похибка найкращого з наближень:
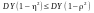 то
то
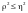 .
.
