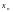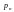- •Дослід, якісна та кількісна характеристика досліду. Неможлива та достовірна події.Протилежна подія.
- •Сума, добуток, різниця подій. Несумісні події. Повна група несумісних подій.
- •Частота та відносна частота події. Властивості відносних частот.
- •Статистична ймовірність події. Аксіоми теорії ймовірностей. Вимірювання ймовірності на практиці.
- •Властивості ймовірностей.
- •Умовна відносна частота. Відносна частота добутку подій. Умовна ймовірність події. Формула множення ймовірностей та формула для умовної ймовірності.
- •Залежні та незалежні події. Теорема множення для незалежних подій.
- •Простий дослід. Класичне означення ймовірностї. Геометричні ймовірності.
- •Формули комбінаторики.
- •Формула повної ймовірності та формула Байєса.
- •Повторні випробування та формула Бернуллі.
- •Наближені формули до формули Бернуллі.
- •Випадкова величина. Функція розподілу та її властивості.
- •Дискретна випадкова величина. Закон розподілу, полігон, функція розподілу.
- •Абсолютно неперервна випадкова величина, її функція розподілу та щільність розподілу. Властивості щільності.
- •Математичне сподівання випадкової величини та його властивості.
- •Властивості математичного сподівання
- •Дисперсія випадкової величини та її властивості.
- •Властивості дисперсії
- •Моменти, асиметрія, ексцес. Мода, медіана та квантилі.
- •Рівномірний розподіл.
- •Стандартний нормальний розподіл.
- •Нормальний розподіл та його властивості. Центральна гранична теорема.
- •Властивості нормальних розподілів
- •Центральна гранична теорема Ляпунова
- •Показниковий розподіл, його властивості.
- •Біноміальний розподіл.
- •Розподіл Пуассона. Потоки найпростіших подій.
- •Геометричний та гіпергеометричний розподіли. Розподіл Пірсона.
- •Розподіл - Пірсона
- •Нерівність Маркова та Чебишова.
- •Теореми Хінчина, Чебишова та Бернуллі.
- •Двовимірна випадкова величина. Основні означення.
- •Числові характеристики двовимірної випадкової величини.
- •Означення регресії. Теорема про лінійну регресію. Властивості коефіцієнта кореляції.
- •Властивості коефіцієнта кореляції
- •Умовне математичне сподівання та його властивості.
- •Властивості mxy
- •Теорема про умовне математичне сподівання. Властивості кореляційного відношення.
- •Властивості кореляційного відношення
- •Двовимірний нормальний розподіл та його властивості.
- •Означення вибірки, статистики, оцінки параметра, міри розсіювання параметра. Теорема про міру розсіювання.
- •Означення незміщеної, асимптотично незміщеної, конзистентної та ефективної оцінок. Оцінки
- •Оцінка дисперсії. Виправлена дисперсія. Їх властивості.
- •Емпірична функція розподілу. Емпіричний розподіл. Кумулята, полігон, гістограма.
- •Емпіричні оцінки параметрів розподілу та їх властивість.
- •Метод моментів для побудови оцінок.
- •Метод найбільшої правдоподібності.
- •Надійний інтервал. Його побудова, якщо відомий розподіл оцінки параметра.
- •Надійні інтервали для параметрів з стандартно нормально розподіленими оцінками.
- •Надійні інтервали для параметрів нормального розподілу.
- •Асимптотично нормальні оцінки. Приклади та їх надійні інтервали.
- •Поняття критерію згоди. Критерій згоди Пірсона.
- •Перевірка гіпотез з допомогою надійних інтервалів. Метод найменших квадратів.
Формула повної ймовірності та формула Байєса.
Нехай з даним дослідом пов’язана повна група несумісних подій Н1,...,Нn. Їх ще називають гіпотезами. Їхні ймовірності відомі: Р(Н1), Р(Н2),…, Р(Нn). В цьому досліді розглядається подія А, для якої відомі умовні ймовірності при кожній з гіпотез, тобто
РН1(А),..., РНn(А). Потрібно знайти ймовірність події А (кажуть повну ймовірність події А). Р(А)=Р(Н1)РН1(А)+ Р(Н2)РН2(А)+…+ Р(Нn)Рнn(А) – формула повної ймовірності.
РА(Нк)=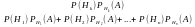 - формула Байєса
- формула Байєса
(рахує ймовірність гіпотези Нк при умові, що сталась подія А)
Повторні випробування та формула Бернуллі.
Нехай проводиться n
незалежних однакових дослідів – повторні
випробування. В кожному з них
спостерігається одна і та ж подія А.
Відома ймовірність
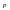 події А в одному досліді. Треба знайти
ймовірність того, що подія А появиться
рівно k разів в цих n
дослідах (0≤ k
≤ n). Ця
ймовірність
позначається
Рn(k).
події А в одному досліді. Треба знайти
ймовірність того, що подія А появиться
рівно k разів в цих n
дослідах (0≤ k
≤ n). Ця
ймовірність
позначається
Рn(k).
Pn(к)=Ckn pk q n - k – формула Бернуллі (q=1-p – ймовірність протилежної події).
Наближені формули до формули Бернуллі.
Фомула Пуассона
Якщо n-дуже велике, k-мале порівняно з n, р теж дуже мале, тоді справедлива формула Пуассона:
Рn(к)≈
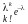 , де
, де
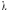 =n*p
=n*p
Локальна формула Лапласа
Коли
п –дуже велике, а
пр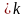 . Тоді
Рn(k)
≈
. Тоді
Рn(k)
≈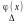 ,
де
,
де
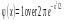 ,
,
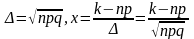 .
.
Інтегральна формула Лапласа
Позначимо Рn(k1,k2) ймовірність того, що подія А станеться в n випробуваннях k разів, де k1≤k≤k2. Тоді Рn(k1, k2)≈ Ф(х2) – Ф(х1)
Ця формула використовується, коли np близьке до k1 і k2 .
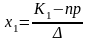 ,
,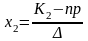 ,
,
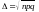
Випадкова величина. Функція розподілу та її властивості.
Величина Х називається випадковою величиною (випадковим розподілом, розподілом), якщо в результаті досліду вона може набувати різних числових значень в залежності від випадку.
Для будь-якого дійсного числа t можна розглядати подію Х< t і знаходити ймовірність цієї події: Р(Х<t) -- ймовірність того, що Х<t. При різних t ймовірності будуть різні, тобто, отримаємо функцію від t, що називається функцією розподілу випадкової величини:
F(t)=FХ(t)=P(Х<t) – означення функції розподілу випадкової величини Х.
Властивості функції розподілу (випливають з властивостей ймовірностей подій)
1.Функція розподілу зростає на R.
2. 0 ≤ F(t) ≤ 1.
3.
F (- ∞)
=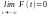 .
.
4.
F (+ ∞)
=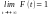 .
.
5.
Функція розподілу неперервна зліва в
усіх точках дійсної прямої
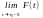 =
=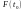 .
.
Дискретна випадкова величина. Закон розподілу, полігон, функція розподілу.
Випадкова величина Х називається дискретною, якщо всі її можливі значення можна пронумерувати. Тоді їх скінченна кількість або стільки, скільки натуральних чисел.
Закон (ряд) розподілу дискретної випадкової величини – це правило, яке всім можливим значенням випадкової величини ставить у відповідність їх ймовірності. Деколи задається формулою, деколи, якщо кількість значень скінченна, задається таблицею:
Х |
х1 |
x2 |
....... |
|
Р |
p1 |
p2 |
|
|
Графік закону розподілу називається многокутником або полігоном розподілу.