
- •Дослід, якісна та кількісна характеристика досліду. Неможлива та достовірна події.Протилежна подія.
- •Сума, добуток, різниця подій. Несумісні події. Повна група несумісних подій.
- •Частота та відносна частота події. Властивості відносних частот.
- •Статистична ймовірність події. Аксіоми теорії ймовірностей. Вимірювання ймовірності на практиці.
- •Властивості ймовірностей.
- •Умовна відносна частота. Відносна частота добутку подій. Умовна ймовірність події. Формула множення ймовірностей та формула для умовної ймовірності.
- •Залежні та незалежні події. Теорема множення для незалежних подій.
- •Простий дослід. Класичне означення ймовірностї. Геометричні ймовірності.
- •Формули комбінаторики.
- •Формула повної ймовірності та формула Байєса.
- •Повторні випробування та формула Бернуллі.
- •Наближені формули до формули Бернуллі.
- •Випадкова величина. Функція розподілу та її властивості.
- •Дискретна випадкова величина. Закон розподілу, полігон, функція розподілу.
- •Абсолютно неперервна випадкова величина, її функція розподілу та щільність розподілу. Властивості щільності.
- •Математичне сподівання випадкової величини та його властивості.
- •Властивості математичного сподівання
- •Дисперсія випадкової величини та її властивості.
- •Властивості дисперсії
- •Моменти, асиметрія, ексцес. Мода, медіана та квантилі.
- •Рівномірний розподіл.
- •Стандартний нормальний розподіл.
- •Нормальний розподіл та його властивості. Центральна гранична теорема.
- •Властивості нормальних розподілів
- •Центральна гранична теорема Ляпунова
- •Показниковий розподіл, його властивості.
- •Біноміальний розподіл.
- •Розподіл Пуассона. Потоки найпростіших подій.
- •Геометричний та гіпергеометричний розподіли. Розподіл Пірсона.
- •Розподіл - Пірсона
- •Нерівність Маркова та Чебишова.
- •Теореми Хінчина, Чебишова та Бернуллі.
- •Двовимірна випадкова величина. Основні означення.
- •Числові характеристики двовимірної випадкової величини.
- •Означення регресії. Теорема про лінійну регресію. Властивості коефіцієнта кореляції.
- •Властивості коефіцієнта кореляції
- •Умовне математичне сподівання та його властивості.
- •Властивості mxy
- •Теорема про умовне математичне сподівання. Властивості кореляційного відношення.
- •Властивості кореляційного відношення
- •Двовимірний нормальний розподіл та його властивості.
- •Означення вибірки, статистики, оцінки параметра, міри розсіювання параметра. Теорема про міру розсіювання.
- •Означення незміщеної, асимптотично незміщеної, конзистентної та ефективної оцінок. Оцінки
- •Оцінка дисперсії. Виправлена дисперсія. Їх властивості.
- •Емпірична функція розподілу. Емпіричний розподіл. Кумулята, полігон, гістограма.
- •Емпіричні оцінки параметрів розподілу та їх властивість.
- •Метод моментів для побудови оцінок.
- •Метод найбільшої правдоподібності.
- •Надійний інтервал. Його побудова, якщо відомий розподіл оцінки параметра.
- •Надійні інтервали для параметрів з стандартно нормально розподіленими оцінками.
- •Надійні інтервали для параметрів нормального розподілу.
- •Асимптотично нормальні оцінки. Приклади та їх надійні інтервали.
- •Поняття критерію згоди. Критерій згоди Пірсона.
- •Перевірка гіпотез з допомогою надійних інтервалів. Метод найменших квадратів.
Надійні інтервали для параметрів з стандартно нормально розподіленими оцінками.
Розглянемо особливості
надійних інтервалів для стандартного
нормального розподілу
N(0;1). Так
як, нормальний розподіл Y дуже поширений,
і він виражається через стандартний: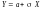 і
навпаки
і
навпаки
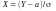 ,
то для побудови надійного інтервалу
для нормального розподілу можна
побудувати його для стандартного
нормального, а потім розв'язати нерівність.
,
то для побудови надійного інтервалу
для нормального розподілу можна
побудувати його для стандартного
нормального, а потім розв'язати нерівність.
Для стандартного нормального
розподілу N(0;1)
квантилі позначаються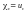 .
.
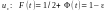
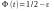 ,
де
,
де
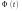 – таблична функція Лапласа (нагадаємо,
що її табличні значення лежать в проміжку
[0; 0,5] ).
– таблична функція Лапласа (нагадаємо,
що її табличні значення лежать в проміжку
[0; 0,5] ).
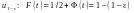
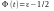 .
.
Оскільки,
– непарна функція, то отримуємо, що
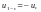 .
.
Отже, двобічний інтервал
надійності
для
розподілу N(0;1)
має вигляд
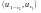 ,
або
,
або
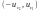 , де
будь- які додатні числа,
для яких
і квантилі
, де
будь- які додатні числа,
для яких
і квантилі
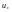 =t
шукаємо з допомогою табличної функції
Лапласа навпаки, прирівнюючи
.
=t
шукаємо з допомогою табличної функції
Лапласа навпаки, прирівнюючи
.
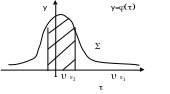
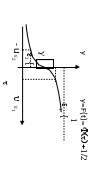
Цей
надійний інтервал буде найточнішим
(найкоротшим), коли
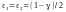 .
Це видно із симетрії щільності N(0;1).
.
Це видно із симетрії щільності N(0;1).
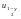 :
:
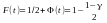
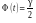 .
.
Отже, найточніший надійний
інтервал надійності
для
розподілу N(0;1)
має вигляд
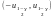 ,
де квантиль
=t
знаходять з табл.ф.Лапласа навпаки,
прирівнюючи
,
де квантиль
=t
знаходять з табл.ф.Лапласа навпаки,
прирівнюючи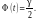
Однобічні інтервали:
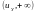 i
i
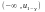 чи
чи
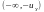 .
.
Надійні інтервали для параметрів нормального розподілу.
Надійні інтервали для
параметрів нормального розподілу можна
використовувати при довільних обсягах
вибірок, не обов’язково великих.
Нормальний розподіл позначаємо
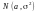 і
його параметри
і
його параметри
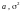 .
.
а) Для
а
при відомому
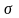 .
.
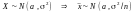 –
тобто,
–
тобто,
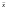 – не тільки асимптотично нормальна
оцінка, а, навіть, просто нормальна
оцінка, така, що завжди має нормальний
розподіл, навіть при малих n.
– не тільки асимптотично нормальна
оцінка, а, навіть, просто нормальна
оцінка, така, що завжди має нормальний
розподіл, навіть при малих n.
Співставимо з
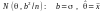 .
.
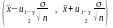 – найточніший інтервал надійності
для
а.
– найточніший інтервал надійності
для
а.
б) Для дисперсії
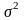 при відомому а.
при відомому а.
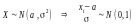 ,
тоді
,
тоді
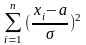 має
розподіл
із n ступенями
вільності. Квантилі
розподілу
із n ступенями
вільності позначаються
має
розподіл
із n ступенями
вільності. Квантилі
розподілу
із n ступенями
вільності позначаються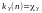 ,
для них складені таблиці.
,
для них складені таблиці.
Тоді, правобічний інтервал
надійності
має
вигляд
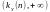 для даного розподілу, тобто,
для даного розподілу, тобто,
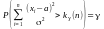
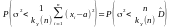 =
,
де
=
,
де
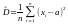 ,
і надійний інтервал для
,
і надійний інтервал для
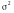 має вигляд:[
має вигляд:[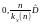 )
–це однобічний інтервал.
)
–це однобічний інтервал.
Аналогічно інший однобічний
інтервал: [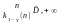 ).
).
Для двобічного беруть
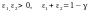 :
:
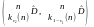
- розподіл не симетричний, то найточніші інтервали шукають методом підбору.
в) Для
при невідомому а.
Можна довести, що
статистика
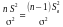 має
розподіл
із n-1 ступенями
вільності.
має
розподіл
із n-1 ступенями
вільності.
Тоді маємо такі інтервали:[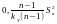 ),[
),[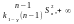 ),
),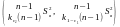 .
.
г) Надійні інтервали для а
при невідомому
.
Можна довести, що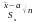 має t-розподіл
Стьюдента із n-1 ступенями
вільності. Маємо надійні інтервали:
має t-розподіл
Стьюдента із n-1 ступенями
вільності. Маємо надійні інтервали:
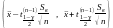
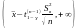
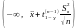 (враховано, що розподіл Стьюдента
симетричний відносно точки 0, з модою
0, як і стандартний нормальний розподіл).
(враховано, що розподіл Стьюдента
симетричний відносно точки 0, з модою
0, як і стандартний нормальний розподіл).
При n>120 заміняють квантилі розподілу Стьюдента t на квантилі стандартного нормального розподілу u.
Асимптотично нормальні оцінки. Приклади та їх надійні інтервали.
Із асимптотично нормальних
оцінок
при
великих обсягах вибірки n
можна побудувати надійний інтервал
для
,
оскільки ми знаємо їх розподіл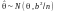 ,
який пов'язаний з числом
.
,
який пов'язаний з числом
.
,
то
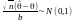 і
інтервал надійності
для
останньої в.в. має вигляд
,
тобто,
і
інтервал надійності
для
останньої в.в. має вигляд
,
тобто,
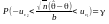 .
Зробимо прості перетворення у внутрішній
нерівності, щоб виразити
:
.
Зробимо прості перетворення у внутрішній
нерівності, щоб виразити
:
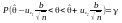 ,
тобто для параметра
отримали
інтервал надійності
:
,
тобто для параметра
отримали
інтервал надійності
:
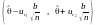 ,
де
будь- які додатні числа,
для яких
і квантилі
=t
шукаємо з допомогою табличної функції
Лапласа навпаки, прирівнюючи
.
,
де
будь- які додатні числа,
для яких
і квантилі
=t
шукаємо з допомогою табличної функції
Лапласа навпаки, прирівнюючи
.
Найточніший надійний інтервал:
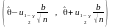 ,
де квантиль
=t
знаходять в таблиці Лапласа навпаки,
прирівнюючи
.
,
де квантиль
=t
знаходять в таблиці Лапласа навпаки,
прирівнюючи
.
Однобічні інтервали (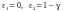 i
i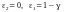 ):
):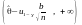 ,
,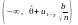 .
.
