40. Метод найбільшої правдоподібності.

Знову ж відомий тип розподілу, але невідомі параметри і їх треба оцінити за вибіркою, тобто виразити їх через .

Знаходимо ймовірність реалізації вибірки ( ), використовуючи відомий тип розподілу Х. Ця ймовірність буде залежати від параметрів 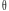=( ) і називається функцією правдоподібності: =

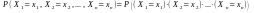=L( , ) =L( , ).

Врахуємо, що експерименти незалежні, тоді – незалежні в.в. з однаковим розподілом Х. L( , )=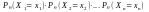 , де формули для ймовірностей беруть з даного типу розподілу, тут дискретного.

Для неперервного розподілу функція правдоподібності має вигляд: L( , )=

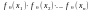= , тобто використовують щільність даного типу.

Метод найбільшої правдоподібності полягає у підборі таких значень параметрів , при яких функція правдоподібності досягає максимуму. Отже, треба знайти точку максимуму функції L від k змінних і координати цієї точки М( ) і будуть шуканими оцінками. Вони будуть залежати від елементів вибірки .

Для знаходження критичної точки складаємо систему рівнянь:

...

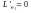
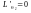
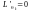
Але, оскільки функція правдоподібності є добутком, то зручніше шукати максимум ln L(x, ). Точки максимуму L і ln L співпадають, бо ln x зростаюча функція.:

...

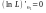
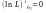
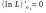
Метод Гауса можна застосовувати лише тоді, коли функція правдоподібності має один максимум.

41. Надійний інтервал. Його побудова, якщо відомий розподіл оцінки параметра.

Надійний інтервал параметра – це інтервал (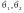 ) з випадковими (залежними від вибірки кінцями), який містить невідомий параметр з ймовірністю не меншою заданого числа 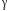. Це число називають надійністю інтервалу: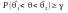 , де 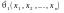, 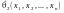– функції від вибірки. вибирають близьке до 1: 0,9; 0,99; 0,95.

Точність надійного інтервалу – це половина його довжини. Чим точніший інтервал з надійністю , тим кращим він вважається.

Але в деяких випадках найкращими вважаються нескінченні надійні інтервали 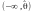, , 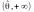вони називаються однобічними, а скінченні – двобічними.

Часто буває відомий розподіл точкової оцінки (чи деякої функції 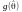), і цей розподіл пов'язаний з невідомим числом (наприклад, як для асимптотично нормальної оцінки). Тоді будують інтервал для розподілу – 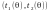, такий, що 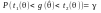– називатимемо його теж надійним інтервалом для розподілу . Потім внутрішню нерівність розв'язують відносно числа і отримують 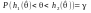, тобто 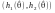– шуканий надійний інтервал для параметра .

Роль функції оцінки може грати будь-яка статистика (функція вибірки), для якої відомий розподіл і він пов'язаний з параметром .

Отже, треба навчитись будувати надійні інтервали для випадкової величини Х з відомим розподілом.

Нехай Х – розподіл з відомою функцією розподілу F(t), чи щільністю розподілу f(t). Потрібно побудувати інтервал 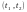, такий, щоб .

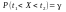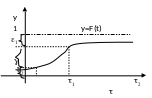
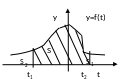
З малюнків: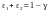 , , 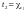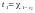; 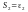S=

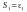
Отже, двобічний інтервал надійності має вигляд 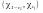, де

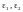будь- які додатні числа, для яких .