Модуль 1.

Додаткові індивідуальні завдання студентів

1. Підприємство випускає продукцію двох видів, використовуючи при цьому сировину трьох типів. Витрати сировини на виробництво продукції задаються матрицею , де –кількість одиниць сировини -го типу, що використовується на виготовлення одиниці продукції -го виду. План щоденного випуску продукції передбачає 90 одиниць продукції першого виду і 120 одиниць продукції другого виду. Вартість одиниці кожного типу сировини відповідно дорівнює 8, 6 і 10 грн. Визначити загальні витрати сировини , необхідні для щоденного випуску продукції, а також загальну вартість С цієї сировини.

2. У цеху підприємства виготовляють дві моделі жіночого одягу. На виготовлення першої моделі витрачають 2 м тканини, на виготовлення другої – 3 м. При цьому витрати робочого часу на виробництво цих моделей становлять відповідно 4 та 5 год. Відомо, що тижневий запас тканини –100 м, а робочий час обмежено 190 год.

Скласти такий план тижневого виготовлення цих моделей одягу, при якому повністю використовують ресурси (тканину і робочий час).

3. Механічний цех може виготовити за зміну або 600 деталей , або 1200 деталей , або будь-яку їхню комбінацію у межах своєї потужності. Виробнича потужність термічного цеху, куди ці деталі надходять для гартування, дозволяє обробити або 1400 деталей , або 800 деталей , або допустиму їхню комбінацію. Деталі надходять після цього у третій цех, пропускна спроможність якого не перевищує 400 деталей.

Записати у математичній формі умови, котрі слід врахувати при складанні плану випуску деталей та . Побудувати область планів випуску деталей та .

4. Знайти ранг матриці:

а) ; б) ;

в) ; г) .

5. Знайти обернену до заданої матриці (якщо вона існує):

а) ; б) ;

в) ; г) .

6. Обчислити визначник, нулі та розкладаючи за елементами рядка або стовпця:

а) ; б) ;

в) ; г) .

7. Обчислити визначник Вандермонда:

а) ; б) .

8. Розв’язати рівняння:

а) ; б) .

9. Розв’язати системи лінійних рівнянь методом Гаусса:

а) 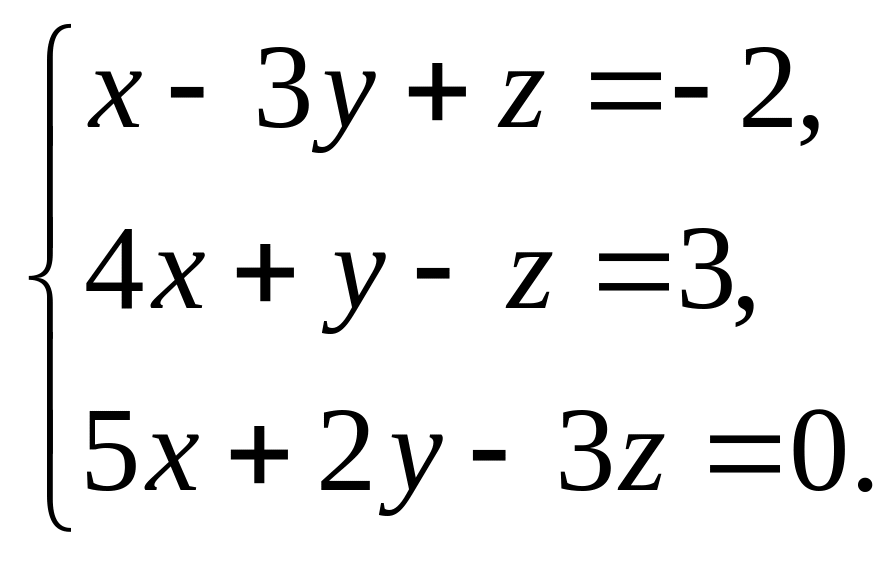б)

в) г)

10. Визначити, при яких значеннях і система

а) має один розв’язок;

б) має безліч розв’язків;

в) не має жодного розв’язку.

11. Розв’язати системи лінійних рівнянь матричним способом:

а) б)

в) г)

12. Знайти довжину висоти трикутника з вершинами , , .

13. Перевірити, чи лежать чотири точки , , і в одній площині.

14. Дослідити взаємне розміщення двох прямих у просторі. Якщо прямі перетинаються, то знайти точку їх перетину.

1) і ;

2) і ;

3) і .

15. Звести до канонічного вигляду рівняння

.

16. Два однотипних підприємства та виробляють продукцію за однаковою гуртовою відпускною ціною за один виріб. Однак автопарк, що обслуговує підприємство , оснащений новішими та потужнішими вантажівками. Тому транспортні витрати на перевезення одного виробу складають за 1 км: для підприємства 10 грош. од., а для підприємства – 20 грош. од. Відстань між підприємствами 300 км. Як територіально має бути поділений ринок збуту між двома підприємствами для того, щоб витрати споживача на відвантаження виробів та їх транспортування були мінімальними?

17. Валова продукція на 1 га сільськогосподарських угідь за чотири роки збільшилась на 24,4 %. Скласти рівняння залежності, яка відображає зміну валової продукції на 1 га протягом чотирьох років за умови, що валова продукція у відсотках змінюється пропорційно часу.

18. Для кривої записати рівняння спряженої гіперболи. Визначити її дійсну та уявну півосі, фокуси, ексцентриситет, рівняння асимптот і директрис.

19. Нехай у момент розпочалося виробництво певного типу машин. Припустимо, що їхній випуск відбувається рівномірно за часом, річний випуск продукції становить 1 млн. грош. од., повний термін експлуатації машин дорівнює 10 років. Визначити вартість машинного парку (за винятком суми зносу) на кінець -го року, .

20. Скласти рівняння параболи з вершиною в початку координат, якщо її директрисою є пряма .

21. Визначити вид і розміщення на площині заданої кривої:

а) ; б) ;

в) ; г) .

22. Дано чотири вектори , , і . Розкласти кожний з цих векторів, приймаючи за базис три інші вектори.

23. Скласти рівняння площини, яка проходить через лінію перетину площин і та перпендикулярна до площини .

24. Задана площина і поза нею точка . Знайти точку , симетричну точці відносно цієї площини.

25. Задана пряма і поза нею точка . Знайти точку , симетричну точці відносно заданої прямої.

26. Через пряму провести площину, паралельну до прямої .

27. Знайти рівняння проекції прямої на площину .

28. Задано точки і . На прямій знайти точку M, яка ділить відрізок у відношенні λ=3.

29. Задано вершини трикутника: А(1; 1; 1), В(5; 1; –2), С(7; 9; 1). Знайти координати точки D перетину бісектриси кута А зі стороною СВ.

30. Скласти рівняння трьох сторін квадрата, якщо відомо, що четвертою стороною є відрізок прямої 4x + 3y – 12 =0, кінці якого лежать на осях координат.