Классификация систем массового обслуживания

Если требование, поступившее в систему массового обслуживания, покидает ее при занятости обслуживающих аппаратов, то такая система называется системой потерей.

Если требования при занятости обслуживающих аппаратов становится в очередь, то такая система называется системой без потерь.

Если число требований, поступающих в систему обслуживания (СМО) не может быть больше определенной величины, то такие системы называются системами с ограниченным потоком требований или замкнутой.

Если число требований не ограничено, то такая (СМО) называется разомкнутой.

Если требования поступающие в СМО удовлетворяются в порядке их поступления, то такая система называется системой без приоритетов.

Если существуют какие-то критерии, с помощью которых очередность удовлетворения требований нарушается, то такая система называется системой с приоритетом.

Показатели качества функционирования смо с неограниченным потоком требований и их оптимизации.

СТО автомобилей индивидуальных владельцев – это система массового обслуживания с ожиданиями (очередь). Число обслуживающих аппаратов ограничено, а число требований в систему не ограничено.

Поток требований и поток восстановления подчиняется закону Пуассона.

1. Вероятность того, что занято точно к обслуживающих аппаратов при условии, что общее число требований находящихся на обслуживании не превосходит число обслуживающих аппаратов.

,

- вероятность того, что все обслуживающие аппараты свободны.

2. Вероятность того, что в системе находится равно К требований в случае когда их число больше числа обслуживающих аппаратов.

3.

4. Среднее число свободных обслуживающих аппаратов .

5. Средняя длина очереди – это среднее число требований ожидающих начала обслуживания .

Рассмотрим пример:

На СТО в сутки поставлено 9 автомобилей.

Время обслуживания 1 автомобиль - 0,5 суток (12 часов).

- выходящий поток.

Выбираем ч – число постов = 5.

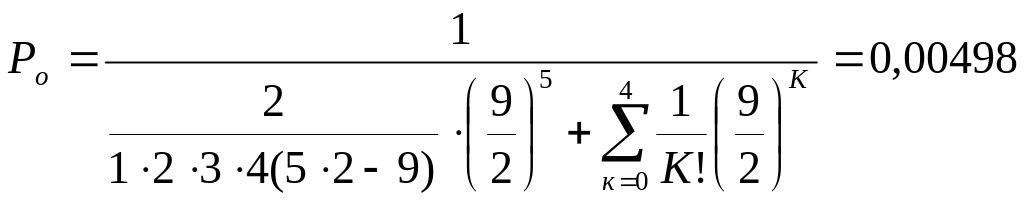
Из Ф(1) при К=Ч имеем:

Из Ф(5) находим длину очереди:

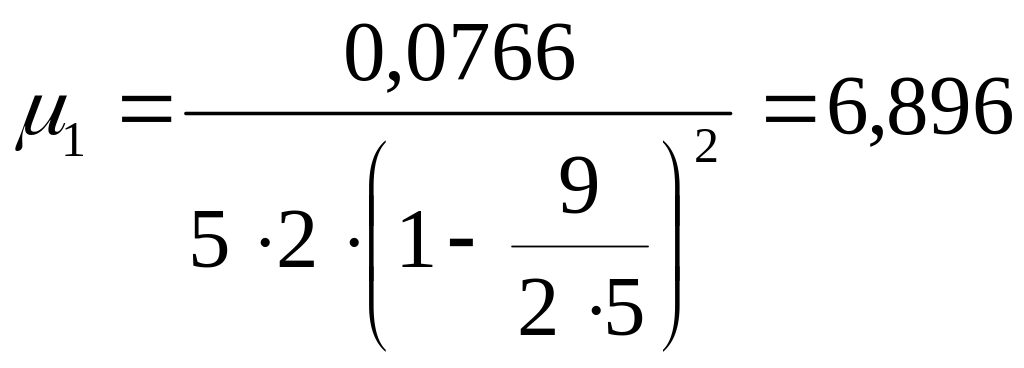
постов.

При решении задачи всегда приходится вводить критерий оптимальности.

Чаще всего используют такой критерий: .

С₁ – издержки (затраты) связанные с простоем ожидания обслуживания одного автомобиля в течение суток.

С₂ – издержки связанные с простоем 1-ого поста в течение суток.

Следовательно, число постов выбирают из условия минимального критерия Э.

С₁ = 30 руб./сут.

С₂= 50 руб./сут.

руб.

Э

Ч отч Ч

Будем решать задачу методом перебора:

ч = 6; Р_о = 0,01; = 1,4 авт.; = 2,5.

ч = 7 Р_о = 0,01; = 04 авт.; = 2,5.

Э = 137 рубл.

Метод Монте Карло и частный случай его критерия для определения потребностей капитального ремонта автомобилей

Пусть в АТП эксплуатируется 300 автомобилей. В среднем за год, каждый автомобиль пробежит 50 тыс. км. Средний пробег до капитального ремонта – 150 тыс. км.

А_сп =300 авт.

ℓ_r= 50 тыс. км. N_к - ?

ℓ_к.р. = 150 тыс. км.

Если бы все автомобили в АТП были новыми, то пробежав каждый в среднем 50 тыс. км. ремонта не потребовали.

Пусть автомобили АТП имеют к концу года пробег от 100 до 150 тыс. км. Значит при пробеге еще 50 тыс. км потребуют капитального ремонта.

Вывод: при расчете числа капитальных ремонтов следует учитывать возраст подвижного состава, который характеризуется пробегом с момента начала эксплуатации.