2.2.2. Методи рішення задач про власні значення на еом
Алгоритми рішення задач про власні значення діляться на дві групи. Ітераційні методи дуже добре пристосовані для визначення найменшого і найбільшого власного значення. Методи перетворень подоби декілька складніше, але дозволяють визначити усі власні значення і власні вектори. До них відносяться метод Якобі, метод Гівенса, метод Хаусхолдера й ін.
Методи рішення розглянутого класу задач входять до всіх стандартних розрахункових пакетів й утримуються в стандартних бібліотеках програм, відкіля і рекомендується вибирати їх інженерам.
Вибір підхожого алгоритму для рішення тієї або іншої задачі на власні значення визначається типом власних значень, типом матриці і числом попрібних власних значень. Одним з ефективних засобів використання стандартного математичного забезпечення є одночасне застосування декількох програм, що дозволяють сполучити їхні кращі якості. Наприклад, маючи матрицю загального вигляду, можна методом Хаусхолдера зводити її до вигляду Хессенберга, а потім за допомогою QR- алгоритму знайти власні значення. Для рішення характеристичного рівняння підходять методи рішення нелінійних рівнянь.
2.2.3. Вправи
Вправа 3. Трьохвісний тензор напруг можна уявити у вигляді матриці 3х3. Для визначення власних значень цієї матриці скласти характеристичне рівняння і звести його до кубічному поліному. Знайти головні напруги якщо:
-
Вариант
Тензор
1
30*106
6*106
5*106
6*106
40*106
7*106
5*106
7*106
20*106
2
10*106
5*106
6*106
5*106
20*106
4*106
6*106
4*106
30*106
3
4,3*106
2,4*106
1,9*106
2,4*106
3,2*106
2,7*106
1,9*106
2,7*106
5,1*106
4
1*106
2*106
1*106
2*106
3*106
2*106
1*106
2*106
1*106
5
15*106
6*106
7*106
6*106
40*106
5*106
7*106
5*106
25*106
6
30*106
5*106
6*106
5*106
45*106
4*106
6*106
4*106
15*106
7
30*106
15*106
7*106
15*106
40*106
10*106
7*106
10*106
20*106
8
40*106
9*106
7*106
9*106
40*106
5*106
7*106
5*106
10*106
Вправа 4. Для довільного тривимірного твердого тіла можна ввести три моменти інерції щодо трьох взаємно перпендикулярних осей і три змішаних моменти інерції щодо трьох координатних площин. Відомо, що для несиметричного тіла при фіксованому початку координат існує єдина орієнтація координатних осей, при якії змішані моменти інерції обертаються в нуль. Такі осі називаються головними осями інерції, а відповідні моменти інерції - головними моментами інерції, серед яких є найбільший, найменший і маючий проміжне значення. Для матриці моментів інерції
4,3 2,4 1,9
2,4 3,2 2,7
1,9 2,7 5,1
знайти три головни момента інерції.
Вправа 5. Баржа призначена для перевозу через морську затоку зчіпки з трьох залізничних вагонів.
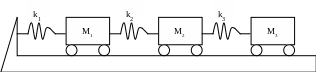
Буксир тягне її за носову
частину. Значення мас вагонів і
коефіцієнтів жорсткості сполучних
елементів задані. Існує застереження,
що в зчіпці вагонів при хвилюванні на
затоці можуть виникнути резонансні
подовжні коливання. Обчислити три власні
частоти даної механічної системи і
порівняти їх із частотою хвилі, рівною
1 рад/с. Власні частоти пов'язані з
власними значеннями динамічної матриці
D співвідношенням wi=
По заданим масам вагонів і жорсткостям зчіпок сформована динамічна матриця D.
1 . 40*109 3*109 0
3*109 3*109 4*109
0 4*109 4*109
2 . 3*109 3*109 0
3*109 3*109 4*109
0 4*109 2*109