2.1.5. Вправи
Вправа 1. Див. умови приклада 1 і 2. Вирішити й одержати рішення. Для обчислення визначників застосувати табличний процесор. Результати роботи зберегти у файлі Впр. 1. Порівняти отримані рішення з приведеними.
Вправа 2. Наведений на малюнку кривошипно-шатунний механізм описується рівняннями
+
-
=
,
при i=1,2,3.
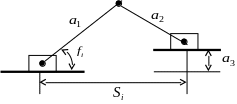
Значення для а задаються формулами:
=
,
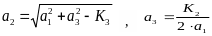
Спроектувати пристрій, що відповідає наступним умовам:
-
Вариант
i
Si
Fi (в градусах)
1
1
1,0
20
2
1,2
45
3
2,0
60
2
1
0,9
30
2
1,1
45
3
1,9
60
3
1
1,1
20
2
1,3
45
3
2,1
60
4
1
1,1
30
2
1,4
45
3
2,2
60
5
1
1,2
30
2
1,5
45
3
2,2
60
6
1
1,0
30
2
1,2
45
3
2,0
60
7
1
1,1
30
2
1,4
45
3
2,0
60
Примітка. Для побудови математичної моделі записати тричі рівняння, що описує роботу механізму і знайти К1,К2,К3 . Провести аналіз отриманих рішень. Для знаходження рішення скористатися табличним процесором і результати роботи зберегти у файлі Впр2_вар.
2.2. Моделі, що зводяться до задач про власні значення
Цілий ряд інженерних задач зводиться до розгляду систем рівнянь, що мають єдине рішення лише в тому випадку, якщо відомо значення деякого вхідного в них параметра. Цей особливий параметр називається власним значенням системи. З задачами про власні значення інженер зштовхується в різноманітних ситуаціях.
Так, для тензорів напруг власні значення визначають головні нормальні напруги, а власними векторами задаються напрямки, пов'язані з цими значеннями.
При динамічному аналізі механічних систем власні значення відповідають власним частотам коливань, а власні вектори характеризують моди цих коливань.
При розрахунку конструкцій власні значення дозволяють визначити критичні навантаження, перевищення яких призводить до втрати стійкості.
2.2.1. Власні вектори і власні значення матриць
Вектор Х
0
називається власним
вектором матриці А,
якщо ця матриця перекладає вектор Х
в вектор л
Х, тобто
А х = n x
Число n називають власним значенням або характеристичним числом матриці А, що відповідає даному власному вектору Х.
Рівняння (1) має ненульове рішення тоді і тільки тоді, коли визначник матриці (А - nЕ) дорівнює нулю: det(А-nЕ) = 0. Цей визначник називають характеристичним визначником матриці А, а рівняння називають характеристичним рівнянням матриці А. У розгорнутому виді це характеристичне рівняння записується в такий спосіб :
(- л)
+с
(-л)
+с
(-л)
+...+с
(-л)+с
=0
Поліном, що стоїть в лівій
частині рівняння зветься
характеристичним
поліномом матриці А. Коеффіцієнт с
дорівнює сумі діагональних елементів
матриці А. Коеффіцієнт с
є сума головних мінорів другого порядку
матриці А Взагалі, коефіцієнт сk
є сума усіх головних минорів к-го порядку
матриці А. І, нарешті, вільний член сn
дорівнює визначнику матриці А. Це
нелінійне алгебраїчне рівняння n-го
ступеня щодо сi-х
і, отже, має, принаймні, один дійсний або
комплексний корінь. Нехай л1,
л2,…, л
, m
n, різноманітні корені рівняння. Ці
корені будуть власними значеннями
матриці А, а сукупність усіх власних
значень звуться спектром
матриці А. При підстановці
кореня л
= л
у рівняння мають
(А- л Е) х = 0
Тому що визначник системи дорівнює нулю, то ця система явно має ненульові рішення, які є власними векторами матриці, що відповідають власному значенню л1.
Якщо корені характеристичного рівняння різноманітні, то кожному власному значенню відповідає з точністю до коефіцієнта пропорційності один і тільки один власний вектор. Власні вектори матриці, що відповідають попарно різноманітним власним значенням, лінійно незалежні.
Матриці, що зустрічаються в інженерних розрахунках, часто бувають симетричними. Тому важливо відзначити, що власні значення симетричної дійсної матриці є дійсними.