2.1.3. Коректність, стійкість, достовірність

Задача зветься коректно поставленою, якщо рішення її існує і єдино при деяких вхідних даних, і стійкою, якщо невеличке відхилення вихідних даних призводить до невеликого відхилення в рішенні. Чутливість рішення до похибки у вихідних даних залежить від гарної або поганої обумовленості системи.

Роздивимося два приклади.

Приклад 1.

Н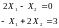 ехай потрібно знайти рішення двох систем лінійних рівнянь, що різняться лише невеличким відхиленням у правій частині системи.

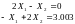
Рішенням перший із них є (1,2), а другий (1.001, 2.002). Похибка в третьому десятковому знаку правої частини викликала зміну теж у третьому знаку в рішенні.

Приклад 2.

В ільні члени системи рівнянь різняться у п'ятій цифрі. Рішенням першої системи буде (17,0) , а рішенням другої - буде (2,3).¹ Усталеність рішення системи до змін вихідних даних у значній мірі залежить від наступного числа:

що називається числом обумовленості матриці системи. Тут знаком - позначені норми матриць.

Якщо число обумовленості матриці невелике, то матриця системи зветься добре обумовленою. У математиці існують формули для підрахунку числа обумовленості через власні значення матриці.

Д остовірність отриманого на ЕОМ рішення визначається формулою, що визначає число обумовленості системи. Ця формула погоджує

властивості матриці системи і похибку в завданні вихідних даних.

У реальних задачах є сенс розглядати ті системи, для яких оцінка числа m помітно менша за одиницю, наприклад, m<0.01. Тут відбивають похибки в матриці та у правих частинах рівняння системи.

2.1.4. Методи рішення лінійних систем на еом

Для рішення систем лінійних алгебраїчних рівнянь застосовуються прямі й ітераційні методи . Прямі методи характеризуються тим, що дають рішення системи за кінцеве число арифметичних операцій. Якщо всі операції виконуються точно (без помилок округлення), то рішення заданої системи теж буде точним (ясно, що це неможливо на ЕОМ).

Ітераційні методи є наближеними. Вони дають рішення системи як послідовність наближень , що обчислюються деяким однаковим процесом. При використанні ітераційного методу завжди передбачається, що на практиці не будується нескінечна послідовність наближень до рішення, а процес зупиняється на якомусь, s-му наближенні, тому в рішенні, отриманому на ЕОМ повинна бути деяка похибка, називана похибкою методу рішення. Джерелом похибки в такому рішенні будуть помилки, що виникають при реалізації чисельних алгоритмів на ЕОМ, тому що всі обчислення виконуються з округленням результатів арифметичних дій до деякої фіксованої кількості розрядів у мантиси чисел.

Внаслідок помилок округлення, що виникають при запровадженні чисел в ЕОМ, точні рішення вихідної системи прямими або ітераційними методами і рішення задачі на ЕОМ можуть відрізнятися.

Сумарний вплив помилок округлення в прямих методах можна розглядати як відповідне еквівалентне відхилення вхідних даних .

Справедливі оцінки :

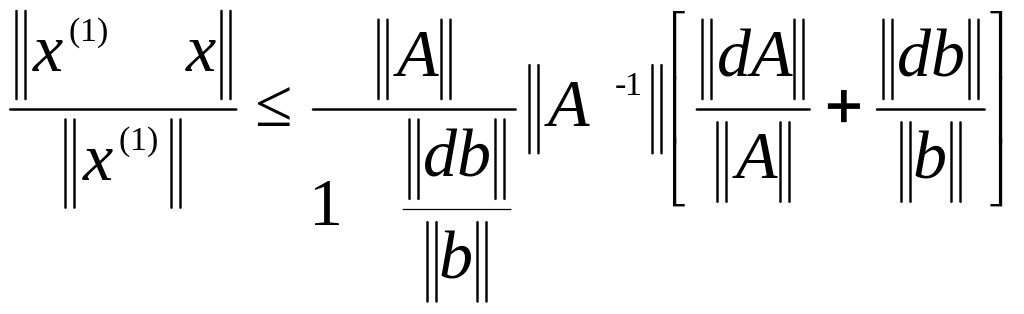,де відхилення даних позначені буквою d.

Оцінки свідчать про те, що помилки машинної реалізації особливо небезпечні для систем лінійних алгебраїчних рівнянь із великими числами обумовленості.

Розгляд оцінок дозволяє зробити висновок про гарну або погану обумовленість системи лінійних алгебраїчних рівнянь у зв'язку з чисельною стійкостю отриманого рішення до сумарних похибок округлення.

Для некоректно поставлених задач побудова рішення звичайними методами, як правило, не призводить до результату.

Інженеру корисно знати, що отриману їм математичну модель задачі у вигляді лінійної системи варто аналізувати для перевірки обумовленості, коректності й стійкості перш ніж розв’язувати її на ЕОМ. У протилежному випадку, машина може видати замість рішення просто ряд цифр, що не має відношення до рішення задачі (див. приклад 1 і приклад 2).

Якщо матриця системи лінійних алгебраїчних рівнянь несиметрична, доцільно використовувати метод Гаусса з вибором головного елемента .

Для рішення систем лінійних алгебраїчних рівнянь із позитивно визначеними матрицями (щільними, стрічкового виду) найкращим є метод, заснований на l -розкладанні. невиродженними Для рішення систем лінійних алгебраїчних рівнянь із невиродженними матрицями довільного вигляду або невиродженними симетричними незнаковизначеними матрицями доцільно застосовувати метод заснований на LU-розкладанні, з тим або іншим вибором головного елементу. Для рішення систем із невиродженною довільною матрицею доцільно використовувати метод Гаусса з вибором головного елемента .

Іноді перед застосуванням прямих методів доцільно провести масштабування системи лінійних алгебраїчних рівнянь (іншими словами, множення матриці зліва і справа на діагональні матриці і відповідну зміну правої частини) із метою зменшення числа обумовленості нової преобразованої матриці.

Вдале масштабування може змінити до кращого спливання обчислювального процесу, що підвищує машинну стійкість рішення до впливу помилок округлення.

Ітераційний метод Якобі (метод простої ітерації) часто реалізується для рішення нескладних лінійних систем. Проте, він має низьку швидкість збіжності.

Виникає необхідність сформулювати такі умови закінчення ітераційного процесу, що забезпечують достатню близькість ітераційного і математичного рішення задачі при доцільному часі рішення.

Виконання умови /condA забезпечує досягнення з точністю до Е близькість обчисленого рішення до шуканого. Схеми для реалізації цих методів наведені в усіх класичних підручниках алгебри, а програми цих методів складають основу бібліотек стандартних програм з рішення лінійних систем. Проте інженеру буде до користі цей підрозділ для того, щоб знати яку програму варто вибрати з стандартної бібліотеки в залежності від вигляду матриці системи. Крім того, очевидна необхідність дослідження властивостей отриманої системи й аналіз її обумовленості перед застосуванням чисельних методів на ЕОМ.