1.3. Обчислювальний експеримент

Поява потужних ЕОМ зробила математичне моделювання потужним інструментом для проведення досліджень і аналізу явищ. У повоєнні роки досягнення фізики і техніки відчинили перспективи реалізації найбільших проектів - освоєння космосу, оволодіння таємницями атомної енергії, пошук нових фундаментальних законів природи.

Якщо раніше проведення експериментів із моделями не виходило за рамки фізичної лабораторії і коштувало щодо недорого, то тепер, перед тим, як вирішитися на постановку дуже дорогого експерименту, треба добре рахувати усе “за” і “проти”.

З появою ЕОМ став можливий обчислювальний експеримент. Його значення важко переоцінити, особливо якщо натурній експеримент небезпечний, дорогий або взагалі неможливий.

Обчислювальний експеримент це моделювання об'єкта на ЕОМ, і якщо модель вірно відображає поведінку об'єкта, то можна “програти” його поведінку в самих різних, часом екстремальних умовах, вибрати найбільше вигідні і зручні параметри. Виникає наступний шлях постановки експерименту:

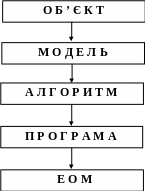
Увесь обчислювальний експеримент умовно можна розділити на наступні етапи.

По-перше, для досліджуваного об'єкту будується фізична модель. Тут відбувається аналіз усіх чинників і поділ їх на головні і другорядні. Одночасно формуються допущення і рамки придатності моделі, у яких будуть справедливі її основні результати.

По-друге, стрворюється математична модель під фізичну модель.

По-третє, розробляється метод розрахунку математичної моделі, тобто обчислювальний алгоритм.

Четвертий етап - це створення програми для реалізації розробленого алгоритму на ЕОМ.

П'ятий етап - проведення розрахунків на ЕОМ.

Шостий етап - опрацювання результатів, їхній всебічний аналіз і висновки.

Тоді під обчислювальним експериментом розуміють дослідження властивостей об'єкта або явища за допомогою рішення на ЕОМ рівнянь, що представляють собою математичну модель об'єкта або явища. Задаючи різноманітним засобом вхідні дані і, розв’язуючи на основі цих даних рівняння, можна зрозуміти роль різноманітних чинників , що визначають досліджувані об'єкти.

Організація і проведення чисельного експерименту висувають вимоги достовірності одержуваних на ЕОМ рішень.

Проблема достовірності містить два аспекти:

• достовірність математичної моделі, що описує прикладну задачу;

• достовірність машинного рішення рівнянь математичної моделі.

Перший аспект, як ми вже згадували, пов'язаний з недообліком тих або інших основних особливостей реального процесу і побудовою неадекватної моделі. Приклад з опадаючим каменем і листком демонстрував цей аспект.

Другий аспект пов'язаний з особливостями реалізації обчислень на ЕОМ і далі буде докладно обговорюватися, що може призвести до утрати всякого змісту в чисельному рішенні математичної моделі.

Таким чином, завжди ставиться задача оцінки близькості машинного рішення до математичного рішення і математичного рішення до фізичного.

Відмова від проведення такого дослідження може привести до того, що отримані результати насправді не будуть являтися рішенням математичної моделі (і тим більше фізичної моделі). Провиною тому буде не метод математичного моделювання як такий, а необачність фахівців у питаннях реалізації математичних моделей на ЕОМ. Формальне застосування математичного апарата може тут привести до помилкових результатів.

Достовірність машинного рішення довгий час (у ранній період застосування обчислювальної техніки) узагалі не аналізувалася. Багато інженерів навіть не підозрювали про те, які «підводні камені» береже недотепне використання обчислювальної техніки.

Суть проблеми, коротко, полягає в наступному:

Для більшості реальних задач, математичні моделі представляють системами диференціальних або нелінійних рівнянь і обмеженнями у виді рівнянь або нерівностей. Вирішити їх аналітичними методами не представляє можливим. Для рішення застосовують чисельні методи, що заміняють початкові неперервні рівняння їхнім дискретним аналогом. На цьому етапі виникає похибка за рахунок чисельної апроксимації операторів початкової задачі. Такі похибки добре вивчені і кожна апроксимація має свій порядок точності.

Реалізація чисельних методів на ЕОМ вносить додаткову погрішність у дискретну модель за рахунок кінцевої арифметиці, яка використовується в машині, оскільки усе величини в машині мають кінцеву розрядність, арифметичні дії виконуються з округленням, погрішності при більших обсягах обчислень накопичуються і починають впливати на результати.

Деякі групи математичних рівнянь, перетворені в машинну модель чутні до таких помилок.

Дослідження в області обчислювальної математики показали, що в ряді випадків удається зазначити ті властивості математичних моделей, що обов'язково потребують аналізу при рішенні цих рівнянь на ЕОМ. При цьому вдається зазначити інтервал у який математичні рівняння, задані з погрішністю, дають коректне рішення чисельними методами. Якщо погрішність завдання початкових даних у рівняннях виходить за рамки цього інтервалу, то при розв'язанні на ЕОМ можливо одержання чисел, що не мають нічого спільного з рішенням задачі.

У курсі «математичні моделі в розрахунках на ЕОМ» будуть розглянуті деякі ситуації для різноманітних класів задач і приведені властивості математичних моделей, що підлягають попередньому аналізу для забезпечення необхідної близькості машинного розв'язання до математичного розв'язання задачі.