2.4.4. Математичні моделі вагонів
Моделі елементів конструкцій вагонів охоплюють значну частину типових розрахункових схем будівельної механіки, що діляться на такі класи:
Стрижні (балки)
Стрижневі системи (ферми, плоскі або просторові рами)
Оболонки (призматичні або обертання) із вирізами або без них
Комбіновані системи
Стрижні і балки використовуються як розрахункові схеми при оцінюванні міцності гальм підоймових передач,віосей колісних пар і других елементів вагонів. Ферми зустрічаються в конструкціях кузовів критих вагонів і піввагонів. Рами використовуються в конструкціях візків, платформ і других типів вагонів. Казани цистерн розглядаються як циліндричні оболонки. Широко поширені підкріплені листові системи. Прикладом може служити конструкція кузова пасажирського вагона, що являє собою оболонку з вирізами, підкріплену набором подовжніх і поперечних елементів.
Конструкції елементів вагонів при упорядкуванні розрахункових схем можуть бути подані у виді окремих стрижнів або системи взаємозалежних стрижнів. Стрижень - це тіло, у якого один із лінійних розмірів значно перевищує другі розміри. Стрижень, підданий впливу поперечних навантажень, називається балкою. Задачі про прогин середини осі колісної пари під дією статичного навантаження зводиться до задачі про вигин балки. Математичні моделі таких задач добре описані і складають основу курсу опору матеріалів. Вигин балки описується диференціальним рівнянням
Підставляючи сюди значення вигибних моментів, маємо систему:
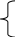
Ця система являє собою математичну модель задачі про прогин середини осі колісної пари. Подальше рішення зводиться до інтегрування рівнянь системи.
Серед множини моделей вагонів широко відома одномасова модель, що дозволяє вивчати вертикальні коливання кузова.
Z
b c
Це одна із самих давніх моделей, що відбиває з деякою наближеністю основні процеси коливань вагона. З цієї моделі починало освоєння основ динаміки рухливого складу не одне покоління інженерів. У умовах стандартних допущень, що кузов являє собою абсолютно тверде недеформоване тіло, маса пружного елемента значно менше маси кузова, пружний елемент є абсолютно пружним і має лінійну характеристику і так далі, диференціальне рівняння для цієї задачі записується у вигляді:
Це лінійне однорідне звичайне диференціальне рівняння другого порядку з постійними коефіцієнтами.
Якщо доповнити умову задачі тим, що вагон рухається по рельсовому абсолютно жорсткому шляху з деякою швидкістю, то в диференціального рівняння з'являється права частина
Це лінійне неоднорідне звичайне диференціальне рівняння другого порядку.
2.4.5. Рішення звичайних диференціальних рівнянь
У залежності від числа незалежних перемінних і, отже, типу вхідних похідних диференціальні рівняння діляться на звичайні, що містять одну незалежну змінну, і рівняння в часткових похідних, що містять декілька незалежних змінних і похідних по ним.
Щоб вирішити звичайне диференціальне рівняння, необхідно знати значення залежної змінної і її похідних при деяких значеннях незалежної змінної. Якщо ці умови задаються при однім значенні незалежної перемінної, то така задача називається задачею з початковими умовами або задачею Коші. Якщо ж умови задаються при двох або більш значеннях незалежної перемінної, то задача називається крайової. У задачі Коші додаткові умови називають початковими, а в крайовій задачі - граничними. Часто в задачі Коші в ролі незалежної перемінної виступає час. Прикладом може служити задача про вільні коливання тіла, підвішеного на пружині. Рух такого тіла описується диференціальним рівнянням, у якому незалежної перемінної є час. Якщо додаткові умови задані у виді значень переміщення і швидкості при t=0 , то маємо задачу Коші. Для тієї ж механічної системи можна сформулювати і крайову задачу. У крайових задачах часто незалежної перемінної виступає довжина. Прикладом може служити задача про деформацію пружного стрижня. У цьому випадку граничні умови звичайно задаються на обох кінцях стрижня. При рішенні задач Коші і крайових задач застосовуються різні методи і обчислювальні алгоритми. Найбільше поширеними серед інженерів методами рішення крайових задач є кінцево-різницеві методи. Вони також застосовуються для рішення диференціальних рівнянь у часткових похідних, тому відкладемо їхній розгляд до відповідного розділу.
Роздивимося методи рішення задач Коші який називаються одношаговими методами.
Одношагові методи для знаходження такої точки на кривій y=f(x) потребують інформації лише про один попередній крок і призначені для рішення диференціальних рівнянь першого порядку вигляду
y’=f(x,y),
де y’=dy/dx , при початковій умові y(x0)=y0. За допомогою цих методів обчисляють послідовні значення в, що відповідають дискретним значенням незалежної змінної х. До одношагових відносяться метод Эйлера і метод Рунге-Кутта.