48

КАФЕДРА АТЗ

МАТЕМАТИЧНІ МОДЕЛІ У РОЗРАХУНКАХ НА ЕОМ

Учбовий посібник

2002

ЗМІСТ

Введення

Одним із відомих методів дослідження і рішення прикладних технічних задач є моделювання. Моделювання використовується при проектуванні і створенні різноманітних систем. За допомогою моделювання аналізують як роботу окремих елементів об’єкту, так і процес взаємодії цілого об'єкта з іншими системами. Чим більше модель враховує різноманітні фактори впливу, тим більше складними рівняннями вона описується.

Математичному опису складних фізичних явищ і процесів із різноманітних галузей життя присвячена множина підручників по класичних інженерних дисциплінах: опір матеріалів, теоретична механіка, механіка тіл що деформуються і ін. Усі вони містять математичні моделі добре вивчених фізичних процесів. Математичні рівняння, що входять у них, складають основу довідників по відповідних розділах фізики.

Розвиток обчислювальної техніки дозволило різко збільшити складність математичних моделей і прискорити процес одержання їх рішення. Проте, саме застосування чисельних методів на ЕОМ призвело до необхідності аналізу отриманих на машині рішень і суворого обґрунтування вибору чисельного методу при рішенні задачі.

Той факт, що в ряді випадків інженер може не підозрювати, що видане машиною число не є рішення математичної моделі явища, а тим більше рішення фізичної моделі , призвів до необхідності привернути увагу інженерів до особливостей рішення математичних моделей на ЕОМ.

Цим обумовлена поява в курсі для технічних спеціальностей дисципліни «Математичні моделі в розрахунках на ЕОМ».

У запропонованому посібнику почата спроба, у доступній формі познайомити студентів із поняттями математичного моделювання, описати основні математичні моделі, що зустрічаються в задачах міцності і при розрахунку будівельних конструкцій, зазначити основні чисельні методи рішення виникаючих математичних рівнянь і особливості їхньої реалізації на ЕОМ. Матеріал жадає від студентів знань по курсам математики, фізики й опору матеріалів в обсязі програм для Втузів.

Розділ 1. Загальні питання теорії моделювання

1.1. Поняття моделі в прикладному дослідженні

Для рішення прикладних задач достатньо поширений метод побудови моделей. Щоб використовувати математичні методи для аналізу реальних процесів, необхідно деякий математичний опис цих процесів, тобто опис на мові математики. Цей математичний опис ми і називаємо математичною моделлю.

На практиці часто буває, що одних лише математичних пізнань далеко не достатньо, щоб вирішити ту або іншу прикладну задачу. Необхідно ще навички в перекладі вхідного формулювання задачі на математичну мову. У цьому і складається проблема оволодіння мистецтвом математичного моделювання. Цим пояснюється поява в традиційних курсах дисципліни, головною ціллю якої є навчання методам постановки математичних задач, що виникають у реальних практичних ситуаціях - математичному моделюванню.

Реальна ситуація рідко буває чітко обкреслена, а складна взаємодія з навколишнім середовищем часто робить точний опис ситуації скрутним. Паралельно з постановкою задачі йде процес виявлення основних або істотних особливостей явища: деякі риси явища визначаються важливими, а багато інших - несуттєвими.

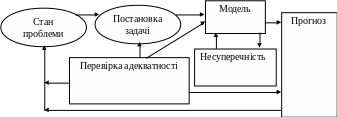
Часто думають, що створення математичних моделей і проведення обчислювальних експериментів на їхній основі - справа математиків. Це не вірно. Адже рівняння, що лежать в основі математичної моделіи - це записані на мові цифр і символів основні закономірності явища. Хто знає їх краще, чим спеціаліст? Гарна модель - це плід співробітництва математика і спеціаліста і щоб таке співробітництво було плідним, вони повинні розуміти один одного. Тому з вузівської лавки студенти повинні навчатися побудові математичних моделей своєї галузі.

Саме поняття «моделювання» звичайно зв'язують із створенням спрощеного опису процесу або системи для полегшення їхнього аналізу. Модель у тому або іншому змісті, більш-менш повно імітує оригінал. Опис може бути якісним або кількісним. Проте в будь-якому випадку його характерна риса складається в тому, що воно не відсвічує цілком усі характеристики досліджуваної системи, воно в цілому простіше об'єкта.

ВИЗНАЧЕННЯ. Об'єкт А є моделлю об'єкта В по відношенню до деякої системи характеристик S, якщо А будується для імітації В по цих характеристиках.

Модель може бути побудована як для вивчення зазначених характеристик (дослідницькі моделі), так і для їхнього безпосереднього використання (робітницькі моделі: автопілот, протез, лялька, гроші).

Дослідницькі моделі можна підрозділити на дві групи:

• експериментальні (предметні)

• теоретичні (умоглядні).

Експериментальні моделі являють собою реально існуючі устрої двох типів: моделі першого типу мають ту же природу, що і об'єкт що моделюється, але відтворюють його спрощено і, звичайно, у зміненому масштабі. У основі моделювання лежить теорія подоби, що підтверджує, що абсолютна подоба може мати місце лише при заміні одного об'єкта іншим точно таким же. Абсолютної подоби при моделюванні не існує, звичайно прагнуть до тому, щоб модель достатньо добре відображала досліджувану сторону функціонування об'єкта. Подоба здійснюється по тим параметрам, що істотні для досліджуваних характеристик: наприклад, для дослідження опору прямуванню об'єкта потрібна модель, зовнішні форми якої подібні оригіналу, а для дослідження міцності того ж об'єкта - модель, що імітує його силовий каркас. Такі моделі іменуються фізичними. У якості одного з ознак класифікації видів моделювання використовують ступінь повноти моделі, і поділяють моделі на повні, неповні і наближені. У основі повного моделювання лежить повна подоба як у часу, так і в просторі. Для неповного моделювання характерно неповна подоба моделі самому досліджуваному об'єкту. У основі наближеного моделювання лежить наближена подоба, при котрої деякі сторони функціонування реального об'єкта не моделюються зовсім.

Так, наприклад, еквівалентна схема електронної лампи - це модель. Проте модель, що правильно описує співвідношення між током і напругою усередині приладу з деяким припустимим ступенем наближення, практично не дає інформації про фізичні розміри лампи або про навколишні умови, у яких вона повинна працювати. Таким чином, процес створення моделі або опису фізичної системи в більшій або меншій мірі складається в абстрагуванні від реальної системи.

Експериментальні моделі іншого типу - аналогові моделі - засновані на збігах математичного опису різноманітних явищ. Так, наприклад, коливальні явища в механічних і електричних системах описуються однаковими диференціальними рівняннями; це дозволяє замість щодо складного експерименту на механічній моделі поставити більш простий експеримент на відповідній електричній моделі, що у даному випадку і виступає в ролі аналога.

Застосовуються також комбіновані пристрої, що об'єднують моделі одного й другого типу - гібридні моделі.

Теоретичні моделі формулюються на мові тієї або іншої науки:

• математичні моделі

• фізичні моделі

• економічні моделі і т.д.

Теоретичні фізичні моделі імітують реальний об'єкт за допомогою абстрактних уявлень на фізичній мові, часто з використанням засобів математики. Після того, як теоретична фізична модель утворена, переходять до побудови математичної моделі.

Математичною моделлю задачі служить система рівнянь у самому широкому змісті цього терміна. Математичне моделювання для дослідження характеристик процесу ділиться на аналітичне, імітаційне і комбіноване.

Аналітичне моделювання відбиває процеси функціонування елементів системи у вигляді деяких функціональних співвідношень (алгебраїчних, интегро-диференціальних і т.д.) або логічних умов. Аналітична модель може бути досліджувана такими методами:

• аналітичним, коли прагнуть одержати в загальному вигляді явні залежності для шуканих характеристик;

• чисельним, коли, не уміючи вирішити рівняння в загальному вигляді, прагнуть одержати числові результати при конкретних початкових даних;

• якісним, коли, не маючи рішення в явному вигляді, можна знайти деякі властивості рішення (наприклад, оцінити усталеність).

Імітаційне моделювання реалізує алгоритм, що відтворює процес функціонування системи в часу, причому імітуються елементарні явища, що укладають процес, із зберіганням їхньої логічної структури і послідовності протікання в часу, що дозволяє по вихідним даним одержати зведення про стани процесу у визначені моменти часу, що дають можливість оцінити характеристики системи. У порівнянні з аналітичним моделюванням імітаційне дозволяє вирішувати більш складні задачі, тому що імітаційні моделі дозволяють достатньо просто враховувати наявність дискретних і безупинних елементів, нелінійні характеристики елементів системи, випадкові впливи і т.д., що дуже важко врахувати при аналітичних дослідженнях. Імітаційне моделювання дозволятити вирішувати задача аналізу великих систем, включаючи задачі оцінки: варіантів структури системи, ефективності різноманітних алгоритмів керування системою, впливи різноманітних параметрів системи. Імітаційне моделювання використовують при структурному, алгоритмічному синтезі великих систем, коли потрібно створити систему з заданими характеристиками при визначених обмеженнях, що є оптимальної по деяких критеріях оцінки ефективності.

Комбіноване моделювання проводить попередню декомпозицію процесу функціонування об'єкта на складові підпроцеси, і для тих із них, де це можливо, використовуються аналітичні моделі, а для інших будуються імітаційні моделі. Це дозволяє охопити якісно нові класи систем, що не можуть бути досліджувані з використанням тільки аналітичного й імітаційного моделювання окремо.

Методи моделювання діляться на аналогові, цифрові і комбіновані аналого-цифрові. Аналогове моделювання характеризується насамперед використанням неперервних сигналів і елементів. Аналогове моделювання може бути як фізичним, так і математичним. Використовується три форми фізичного моделювання: масштабні моделі, моделі-аналоги й іспити частин систем. Математичні моделі досліджуваної системи являють собою систему рівнянь, розв'язуваних за допомогою блоків аналогової обчислювальної машини. Цифрове моделювання також може бути як фізичним, так і математичним, але математичне моделювання є більш загальним. Цифрове моделювання здійснюється на універсальних ЦОМ. Процес підготування до моделювання виконується відповідно до загальних правил, пов'язаними з програмуванням будь-якої задачі на ЦОМ.

Види моделювання, у залежності від характеру досліджуваних процесів у системі, можуть бути розділені на детерміновані і стохастичні, динамічні і статичні, неперервні, дискретні і дискретно-неперервні.

Детерміноване моделювання відображає детерміновані процеси, тобто процеси, у яких передбачається відсутність усяких випадкових впливів.

Стохастичне моделювання відображає імовірні процеси і події. У цьому випадку аналізується ряд реалізацій випадкового процесу й оцінюються середні характеристики тобто набір однорідних реалізацій.

Статичне моделювання служить для опису поводження об'єкта в якийсь момент часу.

Динамічне моделювання відображає поводження системи в часу.

Дискретне моделювання служить для опису процесів, що передбачаються дискретними, неперервне - дозволить відобразити безперервні процеси в системах, а неперервне-дискретне використовується для випадків, коли хочуть виділити наявність як безперервних, так і дискретних процесів.

Математичне моделювання здійснюють на базі математичного опису реального процесу побудовою математичної моделі (систем рівнянь), що дає в якості рішення ті ж результати, що і при моделюванні на лабораторній моделі. Правильно побудована математична модель відбиває (у визначених рамках) характеристики аналізованого реального процесу.

Межа існування математичної моделі цілком визначаються допущеннями, прийнятими при її побудові. Не урахування основних особливостей (допущень) реального процесу може призвести до помилкових моделей і зрадливих висновків. У даному випадку говорять, що модель не адекватно відбиває процес, що моделюється.

І так, модель повинна бути адекватної досліджуваному реальному процесу щодо обраної системи його характеристик.

При проектуванні моделі необхідно мати повний і добре визначений перелік допущень, на яких будується модель, а потім, визначив їхній вплив на результат моделювання, виявити ті з них, що являються домінуючими. Так, наприклад, одним із поширених допущень являється допущення про відсутність у системі люфтів, зон нечуткості, надмірних перевантажень, у механікові при моделюванні широко використовуються поняття матеріальної точки, абсолютно твердого тіла, пружної або пластичної середи, грузлої рідини. При моделюванні постановок задач користуються допущеннями про абсолютно гладкі або шорсткуваті поверхні і т.п.

Існують спеціальні науки для одержання систем математичних рівнянь, що описують неперервні фізичні процеси (рівняння математичної фізики, опір матеріалів, ТОЭ):

• у механіці закони Ньютона і співвідношення діючих на вільні тіла сил призводять до системи диференціальних рівнянь другого порядку, що описують динаміку системи;

• рівняння Лагранжу призводять до системи сумісних рівнянь, що описують динаміку механічних систем. Якщо рівняння Ньютона і Лагранжа записати в однакових координатах, то одержимо однакові системи рівнянь;

• метод Шредингера дає систему диференціальних рівнянь, що описують явища і динаміку поведінки частинок у квантовій механіці.

Таким чином, закони Ньютона, рівняння Лагранжа і метод Шредингера являються основними методами одержання математичних описів механічних систем.

Незважаючи на те, що фізичні закони описуються відповідними рівняннями, що являються математичними моделями динаміки цих процесів, не всі математичні моделі можуть бути отримані безпосередньо з фізичних законів. Багато систем моделюють за допомогою проведення лабораторних експериментів. Проте не завжди в процесі моделювання об'єкту можна ідентифікувати отримані результати в частотної і часової областях. Таким чином одержання емпіричних залежностей представляє собою складну проблему.