
- •Тригонометрические функции. П.1. Синус и косинус. Тангенс и котангенс.
- •П.2. Знаки тригонометрических функций.
- •П.3. Таблица тригонометрических функций.
- •П.4. Свойства тригонометрических функций.
- •П.6. Тригонометрические функции углового аргумента.
- •П.7.Формулы приведения.
- •Функция , её свойства и график.
- •Функция , её свойства и график.
- •Функция , её свойства и график
- •Функция , её свойства и график
- •Тригонометрические уравнения.
- •Повторение по теме: «Тригонометрические формулы. Решение тригонометрических уравнений».
- •Контрольное задание:
- •Задачи для групп продвинутого уровня
- •Опорные карточки для некомпетентных учеников
Функция , её свойства и график.
|
||||||||
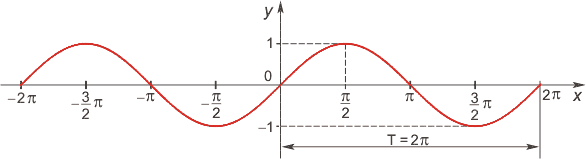
1) Область определения функции — множество R всех действительных чисел,
2) Множество значений функции — отрезок [-1; 1], т.е. синус функция — ограниченная,
3)Функция нечётная: sin(−x)=−sinx для всех х∈ R. График функции симметричен относительно начала координат. 4) Функция периодическая с наименьшим положительным периодом Т = 2π: sin(x+2πk) = sin x, где k∈ Z для всех х∈ R. 5) Нули функции: sin x = 0 при x = πk, k ∈ Z. 6) sin x > 0 (положительная) для всех x∈ (2πk, π+2πk), k ∈Z. sin x < 0 (отрицательная) для всех x∈ (π+2πk, 2π+2πk), k ∈Z. 7) Промежутки монотонности:
|

Функция , её свойства и график.
|
||||||||||||||
|
||||||||||||||
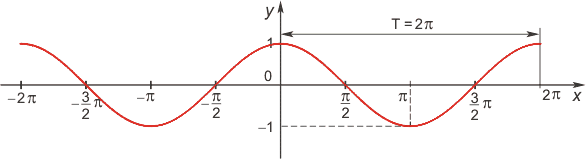
1) Область определения функции — множество R всех действительных чисел. 2) Множество значений функции — отрезок [-1; 1], т.е. косинус функция — ограниченная. 3) Функция чётная: cos(−x)= cos x для всех х ∈ R. График функции симметричен относительно оси Oy. 4) Функция периодическая с наименьшим положительным периодом Т = 2π: cos(x+2πk) = cos x, где k∈ Z для всех х∈ R.
|

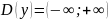
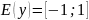
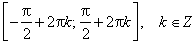

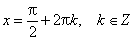

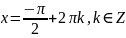 .
.
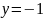 ,
ограничена сверху прямой
,
ограничена сверху прямой
 .
.
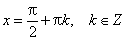
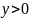 )
для
всех
)
для
всех
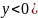 для
всех
для
всех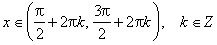
 ,
k
,
k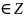
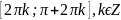
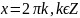 .
.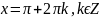 .
.