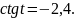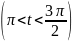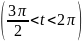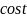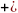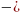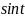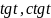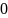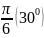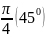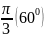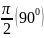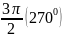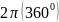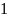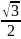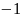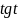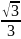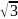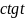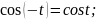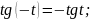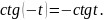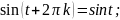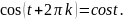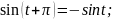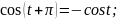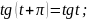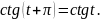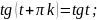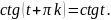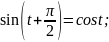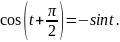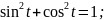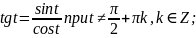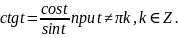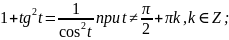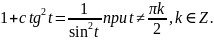z

Тригонометрические функции. П.1. Синус и косинус. Тангенс и котангенс.

Определение 1: Если точка М числовой окружности соответствует числу t, то абсциссу точки М называют косинусом числа t и обозначают cost, а ординату точки М называют синусом числа t и обозначают sint.

Итак,

если M(t) = M(x;y), то x = cost, y = sint.

Отсюда следует, что

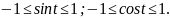
Определение 2: Отношение синуса числа tк косинусу того же числа называют тангенсом числа t и обозначают tgt. Отношение косинуса числа tк синусу того же числа называют котангенсом числа tи обозначают ctgt.

П.2. Знаки тригонометрических функций.

	Четверть окружности
	1-ая	2-ая	3-ая	4-ая

Уравнение числовой окружности имеет вид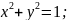 фактически получено важное равенство, связывающее

.

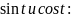
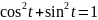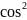t= .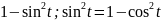

; .

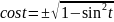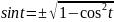П.3. Таблица тригонометрических функций.

t

П.4. Свойства тригонометрических функций.

Свойство 1: Для любого значения tсправедливы равенства:

Свойство 2: Для любого значения tсправедливы равенства:

Свойство 3: Для любого значения t справедливы равенства:

Например, ;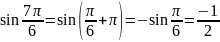

.

Вообще можно записать так:

Свойство 4: Для любого значения tсправедливы равенства:

п.5. Тригонометрические функции числового аргумента.

Каким бы ни было действительное число t, ему можно поставить в соответствие однозначно определённое число sint. Правда, правило соответствия довольно сложное и заключается в следующем. Чтобы по числу t найти sint, нужно:

1. расположить числовую окружность на координатной плоскости так, чтобы центр окружности совпал с началом координат, а начальная точкаА окружности попала в точку (1;0);

2. на окружности найти точку, соответствующую числу t;

3. найти ординату этой точки.

Эта ордината и есть sint.

Фактически речь идёт о функцииs = sint,где t – любое действительное число. Мы умеем вычислять некоторые значения этой функции (например, 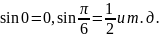), знаем некоторые её свойства.

Точно так же мы можем считать, что уже получили некоторые представления ещё о трёх функциях:s = cost;s = tgt;s = ctgt. Все эти функцииназывают тригонометрическими функциями числового аргумента t.

Есть целый ряд соотношений, связывающих значения различных тригонометрических функций. Некоторые из этих соотношений вы уже знаете:

Из двух последних формул легко получить соотношение, связывающееtgtиctgt:

Пример 1: Упростить выражение:

а) 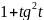; б) .

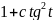Решение.

а)

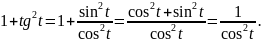
б)

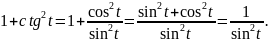
Мы получили ещё две важные формулы:

Пример 2. Известно, что и .

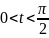Найти соовтетствующие значения cos t, tg t, ctg t.

Решение.

Из соотношения 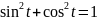находим:

.

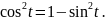
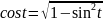, т.к. (1-ая координатная четверть).

Зная значения sin t и cos t, нетрудно вычислить соответсвующие значения tg t и ctg t:

; .

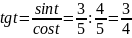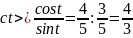Ответ. , , .

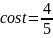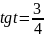Пример 3. Известно, что и .

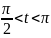Найти:

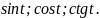
Решение. Из соотношения 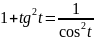находим:

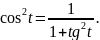
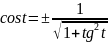
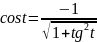, т.к. (2-ая четверть)

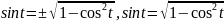
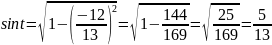
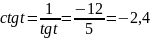
Ответ. ;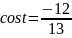

;
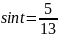