22.Дайте определение генеральной совокупность, выборке.

Генеральной совокупностью называют совокупность всех мысленно возможных объектов данного вида, над которыми проводятся наблюдения с целью получения конкретных значений случайной величины, или совокупность результатов всех мыслимых наблюдений, проводимых в неизменных условиях над одной из случайных величин, связанных с данным видом объектов.

Замечание: Часто генеральная совокупность содержит конечное число объектов. Однако если это число достаточно велико, то иногда в целях упрощения вычислений допускают, что генеральная совокупность состоит из бесчисленного множества объектов. Такое допущение оправдывается тем, что увеличение объема генеральной совокупности (достаточно большого объема) практически не сказывается на результатах обработки данных выборки. Выборка – часть генеральной совокупности, элементы которой подвергаются статистическому изучению; предполагается, что элементы этой части выбраны из генеральной совокупности случайным образом Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности. Например, если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N = 1000, а объем выборки п =100. Число объектов генеральной совокупности N значительно превосходит объем выборки n .

23. Что такое распределение выборки, графическое представление распределений?

Вариационный ряд для дискретного признака X принято наглядно и компактно представлять в виде таблицы, в первой строке которой указаны k различных значений xi изучаемого признака, а во второй строке – соответствующие этим значениям частоты mi , где . Такую таблицу называют статистическим (выборочным) распределением.

24. Что представляет собой эмпирическая функция распределения?

Эмпирической функцией распределения, полученной по выборке , называется функция, при каждом равная где

25. Укажите основные числовые характеристики выборки: среднее арифметическое, мода, медиана, стандартная ошибка, вариационный размах, среднее линейное отклонение, коэффициенты вариации, начальные и центральные моменты, асимметрия, эксцесс. Среднее арифметическое – числовая характеристика совокупности чисел а1, …. аn , определяемая формулой: ā = (а1 + …..+аn) / n. Мода (Мо) – наиболее часто встречающееся в данной совокупности значение признака X. Это варианта с наибольшей частотой. Мода представляет собой максимально часто встречающееся значение переменной (иными словами, наиболее «модное» значение переменной), например, популярная передача на телевидении, модный цвет платья или марка автомобиля и т. д, Сложность в том, что редкая совокупность имеет единственную моду. (Например: 2, 6, 6, 8, 9, 9, 9, 10 – мода = 9). Медиана (Ме) – это серединное значение признака X; которое приходится на середину ранжированного (упорядоченного ряда), по определению: 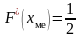. Дисперсия – мера изменчивости для метрических данных, пропорциональная сумме квадратов отклонений измеренных значений от их арифметического среднего (см. таблицу ниже). Поскольку σ – греческая буква, то дисперсию часто просто называют сигма-квадрат, а заглавная греческая буква сигма Σ используется нами как символ, обозначающий суммирование.

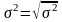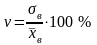Стандартное отклонение (среднее квадратическое) вариационного ряда есть арифметическое значение корня квадратного из дисперсии. R = хmax – хmin - размах вариации. - коэффициент вариации; применяют для сравнения вариации признаков сильно отличающихся по величине, или имеющих разные единицы измерения (разные наименования). Когда график вариационного ряда (распределение набора данных) скошен в правую сторону больше, чем в левую, то мы говорим, что распределение имеет правостороннюю скошенность (асимметрию). Графики вариационных рядов бывают плосковершинными (низковершинными) и островершинными (высоковершинными). Мерой крутости служит эксцесс (куртозис), который характеризует островершинность или плосковершинность ряда распределения. В качестве показателя эксцесса используется величина: Ех = ( µ4 / σ ) – 3. Если Ех > 0, то эксцесс считают положительным (график ряда распределения островершинный), если Ех < 0, то эксцесс считают отрицательным (график ряда распределения плосковершинный).