15. Раскройте сущность понятия «Случайная величина»? приведите пример.
Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее, какое именно.
Примеры случайных величин: 1) число попаданий при трех выстрелах; 2) число вызовов, поступавших на телефонную станцию за сутки; 3) частота попадания при 10 выстрелах.
Во всех трех приведенных примерах случайные величины могут принимать отдельные, изолированные значения, которые можно заранее перечислить.
Так, в примере 1) эти значения: 0, 1, 2, 3; в примере 2): 1,2, 3, 4, …; в примере 3) 0; 0,1; 0,2; …; 1,0. Такие случайные величины, принимающие только отделенные друг от друга значения, которые можно заранее перечислить, называются прерывными или дискретными случайными величинами.
16. Что такое функция распределения? Укажите ее свойства.
Функция распределения – самая универсальная характеристика случайной величины. Она существует для всех случайных величин: как прерывных, так и непрерывных. Функция распределения полностью характеризует случайную величину с вероятностной точки зрения, т.е. является одной из форм закона распределения.
Пусть
дано вероятностное пространство
,
и на нём определена случайная величина
с распределением
. Тогда функцией распределения случайной
величины
называется функция
, задаваемая формулой:
Т.е. функцией распределения (вероятностей)
случайной величины X называют функцию
F(x), значение которой в точке x равно
вероятности события
,
т.е. события, состоящего только из тех
элементарных исходов, для которых
Свойства:
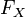непрерывна справа:
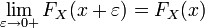
не убывает на всей числовой прямой.
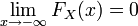
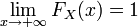
Распределение случайной величины однозначно определяет функцию распределения.
Верно и обратное: если функция
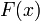удовлетворяет четырём перечисленным
выше свойствам, то существует
вероятностное пространство и определённая
на нём случайная величина, такая что
является её функцией распределения.По определению непрерывности справа, функция имеет правый предел
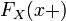в любой точке
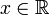, и он совпадает со значением функции
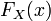в этой точке.
В силу неубывания, функция также имеет и левый предел
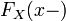в любой точке
,
который может не совпадать со значением
функции. Таким образом, функция
либо непрерывна в точке, либо имеет в
ней разрыв первого рода.
17. Дайте определение понятиям: «Дискретно распределенная случайная величина» и «Непрерывно распределенная случайная величина».
Если случайная величина может принимать конечное или счетное множество значений, то она называется дискретной (дискретно распределенной). Непрерывной случайной величиной называется такая случайная величина, которая может принимать все значения из некоторого конечного или бесконечного промежутка.