10. Что такое формула полной вероятности?
Формула
полной вероятности позволяет вычислить
вероятность интересующего события
через условные вероятности этого
события в предположении неких гипотез,
а также вероятностей этих гипотез.
Формула полной вероятности также имеет
следующую интерпретацию. Пусть —
случайная величина, имеющая распределение
тогда
т.е. априорная вероятность события
равна среднему его апостериорной
вероятности.
11. Приведите формулу Байеса и объясните ее суть.
где,
— априорная вероятность гипотезы A
(смысл такой терминологии см. ниже;
—
вероятность гипотезы A при наступлении
события B (апостериорная вероятность);
—
вероятность наступления события B при
истинности гипотезы A;
—
полная вероятность наступления события
B. Формула Байеса позволяет «переставить
причину и следствие»: по известному
факту события вычислить вероятность
того, что оно было вызвано данной
причиной. События, отражающие действие
«причин», в данном случае обычно называют
гипотезами, так как они — предполагаемые
события, повлекшие данное. Безусловную
вероятность справедливости гипотезы
называют априорной (насколько вероятна
причина вообще), а условную — с учетом
факта произошедшего события —
апостериорной (насколько вероятна
причина оказалась с учетом данных о
событии).
12. В чем заключается формула Бернулли?
Формула
Бернулли — формула в теории вероятностей,
позволяющая находить вероятность
появления события A при независимых
испытаниях. Формула Бернулли позволяет
избавиться от большого числа вычислений
— сложения и умножения вероятностей
— при достаточно большом количестве
испытаний
В формуле Бернулли используется число
сочетаний. ля реализации схемы Бернулли
необходимы два условия: 1) независимость
проводимых испытаний; 2) p = const (постоянное
значение вероятности появления события)
Распределение вероятностей в схеме
Бернулли - биномиальное. Наивероятнейшее
число появления события (мода) при n
испытаниях заключено в пределах np-q ≤
Mo ≤ np+p,
13. Приведите формулу Пуассона и укажите, когда она применима?
Если
вероятность p наступления события А в
каждом испытании постоянна, близка к
нулю, а число независимых испытаний n
достаточно велико, то вероятность Pn(k)
того, что в n независимых испытаниях
событие А наступит k раз, приближенно
равна:
, где λ=np Эта формула называется формулой
Пуассона. Обычно приближенную формулу
Пуассона применяют, когда p<0,1, а npq<10.
Функция
затабулирована, т.е. имеет таблицу.
Значения функции
.
Формула Пуассона используется в задачах,
относящихся к редким событиям.
14. Приведите формулы Муавра-Лапласа и укажите, когда их применяют?
Асимптотические
формулы
Теорема Муавра- Лапласа: Если вероятность
наступления события А в каждом из п
независимых испытаниях равна р и отлична
от 0 и единицы, а число испытаний
достаточно велико, то вероятность
Рп(т)того, что в п испытаниях событие А
наступит т раз,
приближенно равна значению функции
где
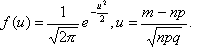
Вычислить
вероятность для каждого случая конечно
можно. Используя рассмотренный метод,
но диапазон довольно велик, поэтому на
практике в подобных случаях для расчетов
применяют формулу, позволяющую вычислить
вероятность для любого диапазона (т1,
т2). Интегральная теорема Муавра- Лапласа:
Если вероятность р наступления события
А в каждом испытании постоянна и отлична
от 0 и 1, то вероятность Рп(т1, т2) того,
что событие А появится в п испытаниях
от т1 до т2 раз. Приближенно равна
определенному интегралу
где
