33. Что представляет собой проверка гипотез о математическом ожидании и дисперсии случайной величины, распределенной по нормальному закону?

В качестве статистического критерия выбирается случайная величина 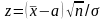, распределенная по нормальному закону, причем Mz = 0 и Dz = 1 ( это следует из свойств математического ожидания и дисперсии ) в случае справедливости гипотезы H₀. Если справедлива гипотеза H₁, то Mz = a* = ( a₁ – a )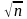 /, Dz = 1. Пусть имеется нормально распределенная случайная величина ,, определенная на множестве объектов некоторой генеральной совокупности. Известно, что D = ². Математическое ожидание M неизвестно. Допустим, что имеются основания предполагать, что M = a, где a – некоторое число (такими основаниями могут быть ограниченные сведения об объектах генеральной совокупности, опыт исследования подобных совокупностей и т. д.). Будем считать также, что имеется другая информация, указывающая на то, что M = a₁, где a₁>a. I. Выдвигаем нулевую гипотезу H₀: M = a при конкурирующей гипотезе H₁: M = a₁.

35. Что такое проверка гипотез о равенстве математических ожиданий и дисперсий?

Пусть имеется выборка n значений нормально распределенной случайной величины: х1, х2, ..., xn. Требуется проверить гипотезу о том, что математическое ожидание х равно определенному значению (обозначим его a). Итак гипотеза Н0: Мх = a. В качестве критерия выбираем случайную величину Очевидно, гипотезу следует отвергнуть и в том случае, если среднее арифметическое много больше а, и в том случае, если среднее арифметическое много меньше а, поэтому критическая область будет двухсторонней, т.е. Q: | t | > tq, так, чтобы Р (| t | ;> tq / H0) = α. По выбранному α и таблице t-распределения находим tq при ν = n - 1; вычисляем , , и tэ по данным эксперимента и принимаем гипотезу, если | tэ | < tq, в противном случае - отвергаем. Алгоритм может быть использован при проверке соответствия теории и эксперимента: в этом случае a - предсказанное теорией значение некоторой физической величины, выборка х1, х2, ..., xn - результаты экспериментального определения той же величины. Этим же приемом пользуемся, чтобы показать, что средство или метод измерения не дают систематической погрешности. В этом случае a- действительное значение некоторой физической величины (свойство стандартного образца или результат измерения заведомо точным прибором, или мировая постоянная), выборка х1, х2, ..., xn ряд результатов, полученных аттестуемым методом (средством) измерения.

36. Раскройте сущность однофакторного и двухфакторного дисперсионного анализа.

Однофакторный дисперсионный анализ применяется для проверки гипотезы о равенстве математических ожиданий нескольких генеральных совокупностей. Такого рода задачи возникают, когда необходимо выяснить оказывает ли на выходную зависимую переменную y влияние входная x, принимающая дискретные значения. ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ БАЗИРУЕТСЯ НА СЛЕДУЮЩИХ ПРЕДПОСЫЛКАХ: 1. В каждом наблюдении ei имеет нормальное распределение с нулевым МО и конечной дисперсией. 2. Для любого i дисперсия ei является величиной постоянной.

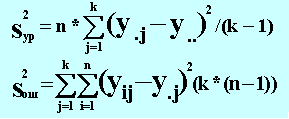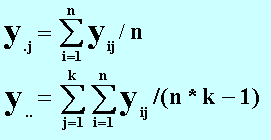где: y.j - среднее по j-му уровню, y.. - общее среднее.

В двухфакторном дисперсионном анализе проверяется гипотеза о равенстве математических ожиданий выходного контролируемого параметра y при различных уровнях двух факторов. ДВУХФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ БАЗИРУЕТСЯ НА СЛЕДУЮЩИХ ПРЕДПОСЫЛКАХ: 1. В каждом наблюдении ei имеет нормальное распределение с нулевым МО и конечной дисперсией. 2. Для любого i дисперсия ei является величиной постоянной.

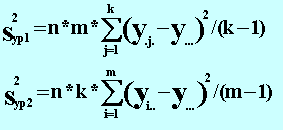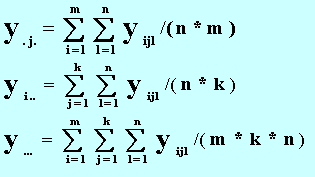где: где: y.j. - среднее по j-му уровню первого фактора, yi.. - среднее по j-му уровню второго фактора, y... - общее среднее

37. Напишите критерии согласия Пирсона, Романовского, Колмогорова.

Критерий согласия Пирсона. Критерием согласия называется критерий проверки гипотезы о

предполагаемом законе неизвестного распределения. С помощью критерия Пирсона можно проверить гипотезу о различных законах распределения генеральной совокупности (равномерном, нормальном, показательном и др.) Для этого в предположении о конкретном виде распределения вычисляются теоретические частоты i n′ , и в качестве критерия выбирается случайная величина

где k – число групп, на которые разбито эмпирическое распределение, – наблюдаемая частота признака в i-й группе, – теоретическая частота. Для распределения составлены таблицы, где указано критическое значение критерия согласия для выбранного уровня значимости и степеней свободы df.(или ). Уровень значимости – вероятность ошибочного отклонения выдвинутой гипотезы, т.е. вероятность того, что будет отвергнута правильная гипотеза. В статистике пользуются тремя уровнями: a= 0,10, тогда Р=0,90 (в 10 случаях их 100 может быть отвергнута правильная гипотеза); a= 0,05, тогда Р=0,95; a= 0,01, тогда Р=0,99. Для оценки существенности расчетное значение сравнивается с табличным . Критерий Романовского с основан на использовании критерия Пирсона, т.е. уже найденных значений и числа степеней свободы df: 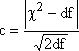.Он удобен при отсутствии таблиц для . Если с<3, то расхождения распределений случайны, если же с>3, то не случайны и теоретическое распределение не может служить моделью для изучаемого эмпирического распределения. Критерий Колмогорова l основан на определении максимального расхождения между накопленными частотами и частостями эмпирических и теоретических распределений: или , где D и d – соответственно максимальная разность между накопленными частотами и накопленными частостями эмпирического и теоретического рядов распределений; N – число единиц совокупности. Рассчитав значение l, по таблице Р(l) определяют вероятность, с которой можно утверждать, что отклонения эмпирических частот от теоретических случайны. Вероятность Р(l) может изменяться от 0 до 1. При Р(l)=1 происходит полное совпадение частот, Р(l)=0 – полное расхождение. Если l принимает значения до 0,3, то Р(l)=1. Основное условие использования критерия Колмогорова – достаточно большое число наблюдений.