24. Закон распределения Пуассона

Дискретная случайная величина имеет распределение Пуассона, если она приобретает зліченної множества значений с вероятностями Это распределение описывает количество событий, которые наступают в одинаковые промежутки времени при условии, что эти события происходят независимо одна от другой с постоянной интенсивностью. Распределение Пуассона рассматривается как статистическая модель для количества альфа-частиц, что их излучает радиоактивный источник за определенный промежуток времени; количества вызовов, которые поступают на телефонную станцию за определенный период суток; количества требований относительно выплаты страховых сумм за год; количества дефектов на одинаковых пробах вещества и т. др. Распределение применяется в задачах статистического контроля качества, в теории надежности, теории массового обслуживания. Математическая надежда и дисперсия в этом распределении одинаковые и равняются а. Для этого распределения сложены таблицы относительно разных значений (0,1 – 20). В таблицах для соответствующих значений а приведено вероятности

Если в схеме независимых повторных испытаний n большое и р или 1 – р следуют к нулю, то биномиальное распределение аппроксимируется распределением Пуассона, когда

Вероятная образующая

Формула Пуассона для самого простого потока

Вероятность того, что за промежуток времени t+?t не состоится ни одно событие, подается в виде

Вероятность того, что за этот самый промежуток времени осуществится т событий, определяется так

Разделим левую и правую части системы уравнений на ?t и выполним предельный переход при ?t -0

В итоге достанем систему линейных дифференциальных уравнений:

25. Геометрическое распределение в теории вероятностей – распределение дискретной случайной величины равной количеству испытаний случайного эксперимента до наблюдения первого «успеха».

Со схемой испытаний Бернулли можно связать еще одну случайную величину x - число испытаний до первого успеха. Эта величина принимает бесконечное множество значений от 0 до + и ее распределение определяется формулой

pk = P(x= k) = qk-1 p, 0 <p <1, k=1, 2, … ,

26. Гипергеометрическое распределение – это дискретное вероятностное распределение, которое описывает количество успехов в выборке без возвращений длины над конечной совокупностью объектов.

Это выборка из объектов, из которых дефектных. Гипергеометрическое распределение описывает вероятность того, что именно дефектных в выборке из конкретных объектов, взятых из совокупности.

Если случайная величина распределена гипергеометрически с параметрами , тогда вероятность получить ровно успехов (дефектных объектов в предыдущем примере) будет следующей:

.

Эта вероятность положительна, когда лежит в промежутке между и .

Приведенная формула может трактоваться следующим образом: существует возможных выборок (без возвращения). Есть способов выбрать бракованных объектов и способов заполнить остаток выборки объектами без дефектов.

В случае, когда размер популяции является большим по сравнению с размером выборки (т.е., намного больше, чем ), гипергеометрическое распределение хорошо аппроксимируется биномиальным распределением с параметрами (количество испытаний) и (вероятность успеха в одном испытании).

Математи́ческое ожида́ние – мера среднего значения случайной величины в теории вероятностей, обозначается через M[X]

Математическое ожидание дискретного распределения

.

27.

Математи́ческое ожида́ние – мера среднего значения случайной величины в теории вероятностей, обозначается через M[X]

Математическое ожидание дискретного распределения

.

Диспе́рсия случа́йной величины́ – мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Обозначается D[X] в русской литературе и (англ. variance) в зарубежной. В статистике часто употребляется обозначение или . Квадратный корень из дисперсии, равный , называется среднеквадрати́чным отклоне́нием, станда́ртным отклоне́нием или стандартным разбросом. Стандартное отклонение измеряется в тех же единицах, что и сама случайная величина, а дисперсия измеряется в квадратах этой единицы измерения.

Из неравенства Чебышёва следует, что случайная величина удаляется от её математического ожидания на более чем k стандартных отклонений с вероятностью менее 1/k². Так, например, как минимум в 75% случаев случайная величина удалена от её среднего не более чем на два стандартных отклонения, а в примерно 89% – не более чем на три.

28. Кроме математического ожидания и дисперсии, для оценки случайной величины используются начальные и центральные моменты случайной величины.

Начальным моментом порядка случайной величины называют математическое ожидание величины :

.

Центральным моментом порядка случайной величины называют математическое ожидание величины :

.

Начальный момент первого порядка равен математическому ожиданию самой случайной величины .

Центральный момент первого порядка равен нулю:

.

Центральный момент второго порядка представляет собой дисперсию случайной величины :

.

Для дискретных случайных величин:

;

.

29. Непрерывная случайная величина в отличие от дискретной случ. величины не может хар-ся вероятностью ее конкретного значения т.к.таких значений бесконечное множество.

Для хар-ки непрерывной случ. величины используеться функция распределения вер-ти, кот. Так же как и для дискретной случ. величины представляет собой вер-ть события, что случ. величина Х принимает значение меньшее определенного х, т.е. F(x)=P(X<x), однако в отличие от дискретной случ. величины Х проходит все непрерывное множество значений, а сама функция F(x) возрастает монотонно. Рассмотрим график функции распределения непр. случ. величины.

В некоторых случаях назначение случ.величины могут быть наложены ограничения , например: время отведенное на выполнение некоторой операции. В этом случае функция распределения будет располагаться лишь в правой полуплоскости. Если случ.величина

Xє[x1;x2], то P(x1<X<x2)=F(x2)-F(x1).

Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х.

Свойства функции распределения

1) значения функции распределения принадлежат отрезку [0, 1].

2) F(x) – неубывающая функция.

при

3) Вероятность того, что случайная величина примет значение, заключенное в интервале (a,b), равна приращению функции распределения на этом интервале.

4) На минус бесконечности функция распределения равна нулю, на плюс бесконечности функция распределения равна единице.

5) Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю.

Таким образом, не имеет смысла говорить о каком – либо конкретном значении случайной величины. Интерес представляет только вероятность попадания случайной величины в какой – либо интервал, что соответствует большинству практических задач.

30. Плотность распределения

Функция распределения полностью характеризует случайную величину, однако, имеет один недостаток. По функции распределения трудно судить о характере распределения случайной величины в небольшой окрестности той или иной точки числовой оси.

Определение. Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения F(x).

Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема.

Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов.

После введения функций распределения и плотности распределения можно дать следующее определение непрерывной случайной величины.

Определение. Случайная величина Х называется непрерывной, если ее функция распределения F(x) непрерывна на всей оси ОХ, а плотность распределения f(x) существует везде, за исключением( может быть, конечного числа точек.

Зная плотность распределения, можно вычислить вероятность того, что некоторая случайная величина Х примет значение, принадлежащее заданному интервалу.

Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a,b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b.

Доказательство этой теоремы основано на определении плотности распределения и третьем свойстве функции распределения, записанном выше.

Геометрически это означает, что вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (a,b), равна площади криволинейной трапеции, ограниченной осью ОХ, кривой распределения f(x) и прямыми x=a и x=b.

№31. Равномерное распределение НСВ: ф-я распр-я, плотность расп-я, график, мат ожидание, дисперсия

Понятие НСВ, функция ее распределения

Случайной непрерывной величиной является величина, которая может принять любое из значений некоторого промежутка. Здесь нельзя отделить одно возможное значение от другого промежутком, не содержащим возможных значений случайной величины.

Случайной непрерывной величиной является величина, функция распределения F(x) которой, непрерывна на всей числовой оси.

Функция распределения HСВ F(x) есть кусочно-дифференцируемая функция с не­прерывной производной.

Вероятность того, что случайная величина примет значение, заключенное в некотором интервале (а,b), равна приращению функции распределения на этом интервале; P(a≤X≤b) = F(b) - F(а).

При рассмотрении функции распределения, числовой промежуток записывается так же в виде [x1; x2], тогда вероятность того, что случайная величина примет значение, заключенное в этом интервале равна:

p(x1≤ x ≤ x2) = F (x2) - F (x1) - что более понятно и привычно.

Вероятность того, что случайная непрерывная величина X примет одно определенное значение, равна нулю.

Понятие плотности распределения, функция плотности НСВ

Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f (х) - первую производную от функции распределения F (х): f (х)= F'(х)

Из этого определения следует, что функция распределения F(х) является первообразной для плотности распределения f (х): F(х)= f (х).

Функцию f (х) можно называть дифференциальной функцией

Таким образом, зная интегральную функцию (функцию распределения) можно найти дифференциальную функцию (функцию плотности) и наоборот по формулам: f (х)= F'(х) F(х)= f (х).

Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл

Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:

При этом, конечно, предполагается, что несобственный интеграл сходится. Свойства математического ожидания НСВ аналогичны свойствам математического ожидания ДСВ.

Дисперсией непрерывной случайной величины называется математическое ожидание квадрата ее отклонения.

По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула:

№32 Нормальное распределение

Это такое распределение случайной величины Х, плотность Р которого опис. Формулой f(x)=(1/(x)*2)*exp(-(x-M(x)2 )/(22(x), где (х)- сред.квадрат.отклонение, М(х)-матем.ожидание

№33 Нормальное расп-е: 1)вероятность попадания в заданный интервал, вероятность заданого отклонения

1)Если случайная величина Х задана плотностью распределения f(x), то вероятность того, что Х примет значение, принадлежащее заданному интервалу, вычисляется по формуле . Подставив в формулу значение плотности распределения из для нормального распределения N(a, s) и сделав ряд преобразований, вероятность того, что Х примет значение, принадлежащее заданному интервалу [x1, x2], будет равна:

где а-мат. ожидание

2)P (|X–a| ≤ e) = 2Ф(/s) = 2Ф(t), где

№34 Показательное расп-е НСВ: график, ф-я расп-я, плотность расп-я, матем ожидание, дисперсия

№35 Показательное расп-е: ф-я надежности, показательный закон надежности, характеристичесткое свойство этого закона

Функция надежности

Будем называть элементом некоторое устройство независимо от того, "простое" оно или "сложное".

Пусть элемент начинает работать в момент времени t0=0, а по истечении времени длительностью t происходит отказ. Обозначим через Т непрерывную случайную величину - длительность времени безотказной работы элемента. Если элемент проработал безотказно (до наступления отказа) время, меньшее t то, следовательно, за время длительностью t наступит отказ.

Таким образом, функция распределения F (t)=P(T<t) определяет вероятность отказа за время длительностью t. Следовательно, вероятность безотказной работы за это же время длительностью t, т. е. вероятность противоположного события Т > t, равна

Функцией надежности R (t) называют функцию, определяющую надежность работы элемента за время длительностью t:

Показательный закон надежности

Часто длительность времени безотказной работы элемента имеет показательное распределение, функция распределения которого

Следовательно, функция надежности в случае показательного распределения времени безотказной работы элемента имеет вид

Показательным законом надежности называют функ­цию надежности, определяемую равенством

где  интенсивность отказов

Как следует из определения функции надежности, эта формула позволяет найти вероятность безотказной работы элемента на интервале времени длительностью tt если время безотказной работы имеет, показательное распределение.

Характеристическое свойство показательного закона надежности.

Показательный закон надежности весьма прост и удобен для решения задач, возникающих на практике. Очень многие формулы теории надежности значительно упрощаются. Объясняется это тем, что этот закон обладает следующим важным свойством: "Вероятность безотказной работы элемента на интервале времени длительностью t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t (при заданной интенсивно­сти отказов )".

Итак, в случае показательного закона надежности безотказная работа элемента "в прошлом" не сказывается на величине вероятности его безотказной работы "в ближайшем будущем".

Замечание. Можно доказать, что рассматриваемым свойством обладает только показательное распределение. Поэтому если на практике изучаемая случайная величина этим свойством обладает, то она распределена по показательному закону. Например, при допущении, что метеориты распределены равномерно в пространстве и во времени, вероятность попадания метеорита в космический корабль не зависит от того, попадали или не попадали метеориты в корабль до начала рассматриваемого интервала времени. Следовательно, случайные моменты времени попадания метеоритов в космический корабль распределены по показательному закону.

№36 Ф-я одного случ аргумента, матем ожидание

Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргумента Х: Y = φ(X). Выясним, как найти закон распределения функции по известному закону распределения аргумента.

1) Пусть аргумент Х – дискретная случайная величина, причем различным значениям Х соответствуют различные значения Y. Тогда вероятности соответствующих значений Х и Y равны.

2) Если разным значениям Х могут соответствовать одинаковые значения Y, то вероятности значений аргумента, при которых функция принимает одно и то же значение, складываются.

3) Если Х – непрерывная случайная величина, Y = φ(X), φ(x) – монотонная и дифференцируемая функция, а ψ(у) – функция, обратная к φ(х), то плотность распределения g(y) случайно функции Y равна:

Математическое ожидание функции одного случайного аргумента.

Пусть Y = φ(X) – функция случайного аргумента Х, и требуется найти ее математическое ожидание, зная закон распределения Х.

1) Если Х – дискретная случайная величина, то

Пример 3. Найдем M(Y) для примера 1: M(Y) = 47·0,1 + 69·0,2 + 95·0,3 + 125·0,4 = 97.

2) Если Х – непрерывная случайная величина, то M(Y) можно искать по-разному. Если известна плотность распределения g(y), то

Если же g(y) найти сложно, то можно использовать известную плотность распределения f(x):

В частности, если все значения Х принадлежат промежутку (а, b), то

№ 37 Ф-я двух случ аргументов, закон расп-я

Если каждой паре возможных значений случайных величин Х и Y соответствует одно возможное значение случайной величины Z, то Z называют функцией двух случайных аргументов X и Y : Z = φ(X, Y).

Рассмотрим в качестве такой функции сумму Х + Y. В некоторых случаях можно найти ее закон распределения, зная законы распределения слагаемых.

1) Если X и Y – дискретные независимые случайные величины, то для определения закона распределения Z = Х + Y нужно найти все возможные значения Z и соответствующие им вероятности.

3) Если X и Y – непрерывные независимые случайные величины, то, если плотность вероятности хотя бы одного из аргументов задана на (-∞, ∞) одной формулой, то плотность суммы g(z) можно найти по формулам

где f1(x), f2(y) – плотности распределения слагаемых. Если возможные значения аргументов неотрицательны, то

Замечание. Плотность распределения суммы двух независимых случайных величин называют композицией.

№38 Закон больших чисел: неравенство Чебышева

В ероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине меньше положительного числа не меньше чем :

p( | X – M(X)| < ε ) ≥ D(X) / ε².

Доказательство. Пусть Х задается рядом распределения

X x1 x2 … xn

P p1 p2 … pn

Так как события |X – M(X)| < ε и |X – M(X)| ≥ ε противоположны, то р ( |X – M(X)| < ε ) + + р ( |X – M(X)| ≥ ε ) = 1, следовательно, р ( |X – M(X)| < ε ) = 1 - р ( |X – M(X)| ≥ ε ). Найдем р ( |X – M(X)| ≥ ε ).

D(X) = (x1 – M(X))²p1 + (x2 – M(X))²p2 + … + (xn – M(X))²pn . Исключим из этой суммы те слагаемые, для которых |X – M(X)| < ε. При этом сумма может только уменьшиться, так как все входящие в нее слагаемые неотрицательны. Для определенности будем считать, что отброшены первые k слагаемых. Тогда

D(X) ≥ (xk+1 – M(X))²pk+1 + (xk+2 – M(X))²pk+2 + … + (xn – M(X))²pn ≥ ε² (pk+1 + pk+2 + … + pn).

Отметим, что pk+1 + pk+2 + … + pn есть вероятность того, что |X – M(X)| ≥ ε, так как это сумма вероятностей всех возможных значений Х, для которых это неравенство справедливо. Следовательно, D(X) ≥ ε² р(|X – M(X)| ≥ ε), или р (|X – M(X)| ≥ ε) ≤ D(X) / ε². Тогда вероятность противоположного события p( | X – M(X)| < ε ) ≥ D(X) / ε², что и требовалось доказать.

№39 Теоремы Чебышева и Бернулли

Теоремы Чебышева и Бернулли.

Рассмотрим последовательность случайных величин (2).

Введем среднее арифметическое:

Запишем математическое ожидание:

Обозначим

Def: говорят, что для последовательности выполняется закон больших чисел, если для любого справедливо равенство:

О равенстве (3) также говорят, что среднее арифметическое случайных величин в вероятностном смысле (по вероятности) сходится к среднему арифметическому их математических ожиданий.

Если последовательность случайных величин (2) удовлетворяет закону больших чисел, то, как видно из равенства (3), среднее арифметическое ведет себя фактически как величина неслучайная, поскольку ее значение в вероятностном смысле как угодно мало отличается от числа (среднего арифметического математического ожидания случайной величины ).

Теорема Чебышева: пусть случайные величины последовательности (2) таковы, что:

1) Они попарно независимы.

2) Имеют конечное математическое ожидание.

3) Имеют равномерно ограниченные дисперсии

Тогда к последовательности применим закон больших чисел.

Доказательство.

Оценим дисперсию:

Применим неравенство (1):

Левую часть выразим через вероятность противоположного события:

Умножим обе части на (-1):

С другой стороны:

На основании двух предыдущих формул получаем формулу (3)

Теорема Бернулли: относительная частота события “А” в вероятностном смысле сходится к вероятности этого события:

(4)

Доказательство.

С каждым испытанием свяжем случайную величину .

Тогда число наступлений события “А” в “n” независимых испытаний будет равно:

Покажем, что к этой последовательности применим закон больших чисел (равенство 3). Проверим выполнение условий теоремы Чебышева:

1) – попарно независимы.

2)

3)

Таким образом в силу теоремы Чебышева к последовательности случайных величин { } применим закон больших чисел, выражаемый равенством (3). В данном случае среднее арифметическое: – относительная частота.

В силу (3) получаем равенство (4).

№40 Оценка отклонения распределения НСВ от нормального коэффициента асимметрии и эксцесса

Коэффициент асимметрии задает степень асимметричности плотности вероятности относительно оси, проходящий через ее центр тяжести. Коэффициент асимметрии определяется третьим центральным моментом распределения. В любом симметричном распределении с нулевым математическим ожиданием, например, нормальным, все нечетные моменты, в том числе и третий, равны нулю, поэтому коэффициент асимметрии тоже равен нулю.

Степень сглаженности плотности вероятности в окрестности главного максимума задается еще одной величиной – коэффициентом эксцесса. Он показывает, насколько острую вершину имеет плотность вероятности по сравнению с нормальным распределением. Если коэффициент эксцесса больше нуля, то распределение имеет более острую вершину, чем распределение Гаусса, если меньше нуля, то более плоскую.

Для расчета коэффициентов асимметрии и эксцесса в MathCAD имеютсядве встроенные функции.

- kurt (x) - коэффициент эксцесса (kurtosis) выборки случайных данных х;

- skew(x) - коэффициент асимметрии (skewness) выборки случайных данных X .

№41 Распределение «хи-квадрат»

Пусть х1, х2,…,хn –независ. Норм. расп-е случ. величины с нулевым матем. ожиданием и сред. квадрат. отклонением = 1,тогда закон расп-я суммы кварт. величин(Х-квадрат) х2=х1 2+х22+…+хn2 назв. Законом Х-квадрат с nстепенями свободы. Плотность расп-я этого закона опред:

0, при х<0

f(x) (e-x/2*xn/2-1)/2n/2+Г’(n/2)x ≥0

№42 распределение Стьюдента

Пусть х0, х1,…,хn – независ. Норм. расп-е случ. величины с нулевым матем. ожиданием и сред. квадрат. отклонением = 1, тогда величина опред по ф-ле:Т=( х0/mn=1*x2/n) назв. Величиной имеющей расп-е Стьюдента с n-степенями свободы

Плотность имеет вид f(x)= bn(1+ x2/2)-((n+1)/n)

bn=Г((n+1)/2)/Гn/2*n

№43 Распределение Фишера-Снедекора

Пусть х1, х2,…,хn ,у1, у2,…,уn независ. Норм.расп-е случ.величины с нулевым матем.ожиданием и сред.квадрат.отклонением=1, тогда случ величина ,заданная ф-лой Fnm=((xi 2/n)/ yj 2/m) назв. Случ величиной, имеющей расп-е Фишера-Снедекора с n и m степенями свободы, плотность расп-я имеет вид

F(x)= 0,при x0

C0 *(x(n-2)/2/(n+n x(+2)/2),для х>0

C0=Г(((n+m)/2)*nn/2 *m m/2 ))Г n/2Г m/2

№44 Система двух случайных величин. Закон расп-я.Ф-я расп-я. Свойства функции расп-я

Законом расп-я назв перечень возможных значений двумерн величины , т.е А(xi,уi) и их соотв. Вероятностей Р (xi,уi). Обычно закон задают таблицей с двойным ходом.1строка-все возможн. значения. составляющие х.1 столбец- все возможн. значения. составляющие у клетки на их пересечении (xi,уi) заполняют соответств. Вероятность, причем кол-во значений х, у могут быть различными, т.к событие х=уi и у=уi образуют полную группу , то сумма вероятностей помещенных во всех клетках =1.

Ф-я расп-я:

Пусть х,у пара действительных чисел, вероятность события состоит в том, что составляющая х примет значение меньше х; составляющая у примет знач-е меньше у. X<x; Y<y. обозначение Р(X<x; Y<y)=F(x;y) – ф-я расп-я

Свойства функции расп-я

1.Значения ф-и расп-я удовлетв. Неравенству 0< F(x;y)<1

2. Ф-я F(x;y) явл. Неубывающей ф-ей.

3. Имеют место след соотношения:1)F(-∞; y)=0 2) F(x;-∞)=0 3) F(-∞;-∞)=0 4) F(+∞;+∞)=1

4. При у=∞, ф-я расп-я с-мы становиться ф-ей расп-я составляющей х. При х=∞, ф-я расп-я с-мы становиться ф-ей расп-я составляющей у

№45 Система двух случайных величин: плотность совместного расп-я вероятностей, нахождение ф-и расп-я по плотности расп-я, свойства двумерной плотности расп-я

Плотность совм.расп-я вероятностей назв частную производную второго порядка, смешанная по переменным х, у

нахождение ф-и расп-я по плотности расп-я

F(x,y)=sinx*siny

0x/2; 0y/2

Решение:

Fх(x,y)=cosx*siny ;Fxy= cosx cosy. Зная плотность расп-я можно найти ф-ю расп-я F(x,y)=-∞∞ -∞∞f(x,y) dx dy

свойства двумерной плотности расп-я:

1.плотность вероятности не отрицательна f(x,y)≥0

2. -∞∞ -∞∞f(x,y) dx dy=1

3. можно найти плотность расп-я для каждой составляющей

46. Определение. Плотностью совместного распределения вероятностей двумерной случайной величины (X, Y) называется вторая смешанная частная производная от функции распределения.

Условные законы распределения составляющих системы дискретных случайных величин.

Рассмотрим дискретную двумерную случайную величину , пусть возможные значения составляющих таковы:

Предположим, что в результате испытания случайная величина Y приняла 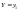значение , тогда X может принять одно из своих возможных значений. Обозначим условную вероятность того, что X примет значение через

Условным распределением случайной величины X при условии, что Y приняла значение называют совокупность условных вероятностей

Зная закон распределения двумерной дискретной случайной величины можно вычислить условные законы распределения составляющих:

Условные законы распределения составляющих системы непрерывных случайных величин

Условной дифференциальной функцией составляющей X при условии, что , называют отношение дифференциальной функции системы к дифференциальной функции составляющей Y.

47. Условное математическое ожидание

Условным математическим ожиданием случайной величины Y при называют сумму произведений возможных значений Y на их условные вероятности.

Для непрерывных величин:

48. Зависимые и независимые случайные величины

Теорема. Для того чтобы случайные величины X и Y были независимы, необходимо и достаточно, чтобы интегральная функция системы была равна произведению интегральных функций случайных величин X и Y.

Следствие. Для того чтобы случайные величины X и Y были независимы, необходимо и достаточно, чтобы дифференциальная функция системы была равна произведению дифференциальных функций случайных величин X и Y.

КОРРЕЛЯЦИОННЫЙ МОМЕНТ Корреляционным моментом двух случайных величин X и Y называют математическое ожидание произведения отклонений этих величин: x y = M{[X - M(X)][Y - M(Y)]}. Корреляционный момент служит для характеристики связи между величинами X и Y. Корреляционный момент двух независимых случайных величин X и Y равен нулю. Если корреляционный момент не равен нулю, то X и Y – зависимые случайные величины. Из определения корреляционного момента следует, что он имеет размерность, равную произведению размерностей величин X и Y. Другими словами, корреляционный момент зависит от единиц измерения случайных величин. Безразмерной числовой характеристикой связи двух случайных величин является коэффициент корреляции.

коэффициент корреляции. Он рассчитывается следующим образом:

Есть массив из n точек {x1,i, x2,i}

Рассчитываются средние значения для каждого параметра:

И коэффициент корреляции:

r изменяется в пределах от -1 до 1. В данном случае это линейный коэффициент корреляции, он показывает линейную взаимосвязь между x1 и x2: r равен 1 (или -1), если связь линейна.

Коэффициент r является случайной величиной, поскольку вычисляется из случайных величин. Для него можно выдвигать и проверять следующие гипотезы:

1. Коэффициент корреляции значимо отличается от нуля (т.е. есть взаимосвязь между величинами):

2. Отличие между двумя коэффициентами корреляции значимо.

49. Генеральная совокупность и выборочная совокупность

В выборочном наблюдении используются понятия «генеральная совокупность» -- изучаемая совокупность единиц, подлежащая изучению по интересующим исследователя признакам, и «выборочная совокупность» -- случайно выбранная из генеральной совокупности некоторая ее часть. К данной выборке предъявляется требование репрезентативности, т.е. при изучении лишь части генеральной совокупности полученные выводы можно применять ко всей совокупности.

Характеристиками генеральной и выборочной совокупностей могут служить средние значения изучаемых признаков, их дисперсии и средние квадратические отклонения, мода и медиана и др. Исследователя могут интересовать и распределение единиц по изучаемым признакам в генеральной и выборочной совокупностях. В этом случае частоты называются соответственно генеральными и выборочными.

Система правил отбора и способов характеристики единиц изучаемой совокупности составляет содержание выборочного метода, суть которого состоит в получении первичных данных при наблюдении выборки с последующим обобщением, анализом и их распространением на всю генеральную совокупность с целью получения достоверной информации об исследуемом явлении.

Репрезентативность выборки обеспечивается соблюдением принципа случайности отбора объектов совокупности в выборку. Если совокупность является качественно однородной, то принцип случайности реализуется простым случайным отбором объектов выборки. Простым случайным отбором называют такую процедуру образования выборки, которая обеспечивает для каждой единицы совокупности одинаковую вероятность быть выбранной для наблюдения для любой выборки заданного объема. Таким образом, цель выборочного метода -- сделать вывод о значении признаков генеральной совокупности на основе информации случайной выборки из этой совокупности.

Типы выборок

Выборки делятся на два типа:

- вероятностные

- невероятностные

1. Вероятностные выборки

1.1 Случайная выборка (простой случайный отбор)

Такая выборка предполагает однородность генеральной совокупности, одинаковую вероятность доступности всех элементов, наличие полного списка всех элементов. При отборе элементов, как правило, используется таблица случайных чисел.

1.2 Механическая (систематическая) выборка

Разновидность случайной выборки, упорядоченная по какому-либо признаку (алфавитный порядок, номер телефона, дата рождения и т.д.). Первый элемент отбирается случайно, затем, с шагом ‘n’ отбирается каждый ‘k’-ый элемент. Размер генеральной совокупности, при этом – N=n*k

1.3 Стратифицированная (районированная)

Применяется в случае неоднородности генеральной совокупности. Генеральная совокупность разбивается на группы (страты). В каждой страте отбор осуществляется случайным или механическим образом.

1.4 Серийная (гнездовая или кластерная) выборка

При серийной выборке единицами отбора выступают не сами объекты, а группы (кластеры или гнёзда). Группы отбираются случайным образом. Объекты внутри групп обследуются сплошняком.

2. Невероятностные выборки

Отбор в такой выборке осуществляется не по принципам случайности, а по субъективным критериям – доступности, типичности, равного представительства и т.д..

2.1. Квотная выборка

Изначально выделяется некоторое количество групп объектов (например, мужчины в возрасте 20-30 лет, 31-45 лет и 46-60 лет; лица с доходом до 30 тысяч рублей, с доходом от 30 до 60 тысяч рублей и с доходом свыше 60 тысяч рублей) Для каждой группы задается количество объектов, которые должны быть обследованы. Количество объектов, которые должны попасть в каждую из групп, задается, чаще всего, либо пропорционально заранее известной доле группы в генеральной совокупности, либо одинаковым для каждой группы. Внутри групп объекты отбираются произвольно. Квотные выборки используются в маркетинговых исследованиях достаточно часто.

2.2. Метод снежного кома

Выборка строится следующим образом. У каждого респондента, начиная с первого, просятся контакты его друзей, коллег, знакомых, которые подходили бы под условия отбора и могли бы принять участие в исследовании. Таким образом, за исключением первого шага, выборка формируется с участием самих объектов исследования. Метод часто применяется, когда необходимо найти и опросить труднодоступные группы респондентов (например, респондентов, имеющих высокий доход, респондентов, принадлежащих к одной профессиональной группе, респондентов, имеющих какие-либо схожие хобби/увлечения и т.д.)

2.3 Стихийная выборка

Опрашиваются наиболее доступные респонденты. Типичные примеры стихийных выборок – опросы в газетах/журналах, анкеты, отданные респондентам на самозаполнение, большинство интернет-опросов. Размер и состав стихийных выборок заранее не известен, и определяется только одним параметром – активностью респондентов.

2.4 Выборка типичных случаев

Отбираются единицы генеральной совокупности, обладающие средним (типичным) значением признака. При этом возникает проблема выбора признака и определения его типичного значения.

Эмпирической функцией распределения, построенной по выборке объема , называется случайная функция , при каждом равная

В отличие от эмпирической функции распределения выборки, функцию распределения генеральной совокупности называют теоретической функцией распределения. Различие между этими функциями состоит в том, что теоретическая функция определяет вероятность события X<x, тогда как эмпирическая – относительную частоту этого же события.

При росте n относительная частота события X<x, т.е. стремится по вероятности к вероятности этого события. Иными словами:

.