
Задание 5
По результатам простой группировки определить взаимосвязь (с использованием дисперсий) между двумя показателями среднегодовая стоимость основных фондов и среднесписочная численность рабочих.
Дисперсионный анализ выполняется на основе расчёта следующих дисперсий:
групповой
межгрупповой
внутригрупповой
общей дисперсии
Для определения тесноты связи между изучаемыми признаками рассчитываются два коэффициента:
коэффициент детерминации
эмпирическое корреляционное отношение
Для нахождения дисперсионного анализа составим вспомогательную таблицу (Таблица 6)
Таблица 6
номер группы |
Среднегодовая стоимость основных фондов, млн руб. |
Количество предприятий |
Номер предприятия |
Среднесписочная численность рабочих |
Сумма |
Среднее |
1 |
180,1 |
7 |
1 |
165 |
1560 |
222,8571 |
294,5 |
2 |
223 |
||||
179,8 |
12 |
184 |
||||
323,4 |
14 |
222 |
||||
228,3 |
17 |
304 |
||||
179,6 |
20 |
275 |
||||
180,4 |
23 |
187 |
||||
2 |
420,8 |
9 |
3 |
545 |
3769 |
418,7778 |
469,7 |
4 |
604 |
||||
426,9 |
5 |
454 |
||||
341,8 |
9 |
442 |
||||
438 |
10 |
214 |
||||
354,2 |
15 |
332 |
||||
367,4 |
18 |
501 |
||||
404,8 |
21 |
211 |
||||
473,3 |
22 |
466 |
||||
3 |
552,4 |
3 |
6 |
504 |
1661 |
553,6667 |
551,5 |
13 |
575 |
||||
551,9 |
16 |
582 |
||||
4 |
664,6 |
1 |
7 |
563 |
563 |
563 |
5 |
784,2 |
5 |
8 |
606 |
3438 |
687,6 |
825,4 |
11 |
704 |
||||
930,3 |
19 |
752 |
||||
828,3 |
24 |
711 |
||||
862,8 |
25 |
665 |
Групповая дисперсия:

Где:
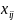 -
значение признака i-ой
единицы j-ой
группы
-
значение признака i-ой
единицы j-ой
группы
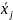 -
групповая средняя величина признака в
j-ой
группе
-
групповая средняя величина признака в
j-ой
группе
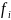 -
вес признака i-ой
группы
-
вес признака i-ой
группы
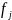 -численность
единиц j-ой
группы
-численность
единиц j-ой
группы
По первой группе:
Среднесписочная численность рабочих |
Число предприятий |
|
|
165 |
1 |
-57,86 |
3347,45 |
223 |
1 |
0,14 |
0,02 |
184 |
1 |
-38,86 |
1509,88 |
222 |
1 |
-0,86 |
0,73 |
304 |
1 |
81,14 |
6584,16 |
275 |
1 |
52,14 |
2718,88 |
187 |
1 |
-35,86 |
1285,73 |
среднее |
222,86 |
сумма |
15446,86 |
 43
43
По второй группе:
Среднесписочная численность рабочих |
Число предприятий |
|
|
545 |
1 |
126,22 |
15932,05 |
604 |
1 |
185,22 |
34307,27 |
454 |
1 |
35,22 |
1240,60 |
442 |
1 |
23,22 |
539,27 |
214 |
1 |
-204,78 |
41933,94 |
332 |
1 |
-86,78 |
7530,38 |
501 |
1 |
82,22 |
6760,49 |
211 |
1 |
-207,78 |
43171,60 |
466 |
1 |
47,22 |
2229,94 |
среднее |
418,78 |
сумма |
153645,56 |

По третьей группе:
Среднесписочная численность рабочих |
Число предприятий |
|
|
504 |
1 |
-49,67 |
2466,78 |
575 |
1 |
21,33 |
455,11 |
582 |
1 |
28,33 |
802,78 |
среднее |
553,67 |
сумма |
3724,67 |
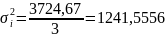
По четвёртой группе:
Среднесписочная численность рабочих |
Число предприятий |
|
|
563 |
1 |
0 |
0 |
среднее |
563 |
сумма |
0 |

По пятой группе:
Среднесписочная численность рабочих |
Число предприятий |
|
|
606 |
1 |
-81,60 |
6658,56 |
704 |
1 |
16,40 |
268,96 |
752 |
1 |
64,40 |
4147,36 |
711 |
1 |
23,40 |
547,56 |
665 |
1 |
-22,60 |
510,76 |
среднее |
687,60 |
сумма |
12133,20 |
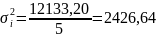
Вывод: изменение среднесписочной численности рабочих за счёт всех факторов кроме среднегодовой стоимости основных фондов:
в первой группе составляет
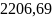 43
чел.
43
чел.во второй-
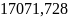 чел.
чел.в третьей -
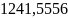 чел.
чел.в четвёртой - 0 чел.
в пятой - 2426,64 чел.
Внутригрупповая дисперсия или средняя из групповых дисперсий:

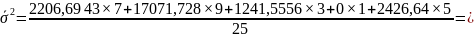 7398,011
7398,011
Вывод: изменение среднесписочной численности рабочих за счёт всех факторов кроме среднегодовой стоимости основных фондов по всей совокупности составляет 7398,011 чел.
Межгрупповая дисперсия или дисперсия средних групповых:
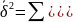
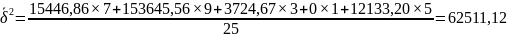
Вывод:
изменение среднесписочной численности
рабочих за счёт среднегодовой стоимости
основных фондов составляет
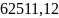 чел.
чел.
Общая дисперсия - дисперсия, вычисленная для всей статистической совокупности в целом как средний квадрат отклонений значений признака от общей средней. Измеряет степень колеблемости признака, порождаемую всей совокупностью действующих на него факторов.
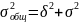
 чел.
чел.
Вывод:
изменение среднесписочной численности
рабочих за счёт всех факторов составляет
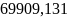 чел.
чел.
Коэффициент детерминации - представляет собой отношение межгрупповой дисперсии к общей дисперсии и показывает, какую часть общей вариации изучаемого признака составляет межгрупповая вариация.
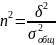
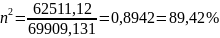
Вывод:
изменение среднесписочной численности
рабочих влияет на изменение среднегодовой
стоимости основных фондов на
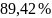 .
.
Эмпирическое корреляционное отношение - показатель тесноты связи между взаимосвязанными явлениями.
ᶯ=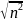
ᶯ= =0,9456
=0,9456
Из значения эмпирического корреляционного отношения видно, что связь между среднесписочной численностью рабочих и среднегодовой стоимостью основных фондов тесная, прямая, так как значение этого отношения положительно и близко к единице.
