
- •Эквивалентное число зубьев колеса и шестерни вычисляем по формулам
- •1.3.3 Ведомый вал
- •1.4 Конструктивные размеры зубчатой пары
- •1.6 Первый этап компоновки.
- •1.7.2 Ведомый вал
- •1.8 Второй этап компоновки.
- •10.3 Проверяемое сечение под колесом ведомого вала
- •10.4 Проверяемое сечение под наиболее нагруженным подшипником ведомого вала
- •10.5 Проверяемое сечение в месте перехода от dп2 под подшипником к dв2 выходного конца ведомого вала. Концентрация напряжений обусловлена переходом от диаметра 75 мм к диаметру 70мм.
1 Расчётная часть
1.1 Выбор электродвигателя и кинематический расчёт
Определяем общий КПД привода по формуле
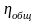 =
=
 (1)
(1)
где
 - потери в зубчатой передаче ;
- потери в зубчатой передаче ;
 [1].
[1].
 -
потери в одной паре подшипников ;
-
потери в одной паре подшипников ;
 [1].
[1].

 -
потери в ремённой передаче;
-
потери в ремённой передаче;
 [1].
[1].
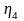 -
потери в муфте;
-
потери в муфте;
 [1].
[1].
=0,98∙0,992∙0,96∙0,98=0,903
Определяем требуемую мощность двигателя Ртр, кВт по формуле
Ртр
= (2)
(2)
где Р3- мощность на ведомом валу редуктора, кВт; Р3= 6 кВт.
Ртр= кВт
кВт
По требуемой мощности Ртр=6,7 кВт и синхронной частоте вращения
nсх =1000 об/мин из каталога электродвигателей ГОСТ 19523 – 81 [1] выбираем двигатель 160М6 с мощностью Рдв=11кВт и скольжением s=3,2%.
Вычисляем число оборотов вала двигателя nдв по формуле
nдв
= nсх
-
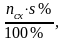 (3)
(3)
где nсх - синхронная частота вращения электродвигателя, nсх =1000
s - скольжение; s=2,7%.
nдв
=1000- об/мин
об/мин
Общее передаточное число привода
uобщ
=
 (4)
(4)
uобщ
=

Передаточное число зубчатой передачи принимаем uзуб =5. Передаточное число ремённой передачи вычисляем по формуле
uрем
=
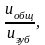 (5)
(5)
uрем
=
Определяем частоту вращения валов привода
-входного вала привода
n1= nдв =968об/мин
 -
ведущего вала редуктора n2
-
ведущего вала редуктора n2
n2
=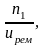 (6)
(6)
n2
= об/мин
об/мин
- ведомого вала редуктора n3
n3
= (7)
(7)
n3=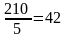 об/мин
об/мин
Угловые скорости валов привода
-входного
вала привода
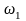 ,
рад/с
,
рад/с
=
= рад/с
рад/с
-
ведущего вала редуктора ,
 ,
рад/с
,
рад/с
=
= рад/с
рад/с
-
ведомого вала редуктора ,
 ,
рад/с
,
рад/с
 3
=
3
=

= рад/с
рад/с
Вычисляем вращающие моменты на валах привода
-входного вала привода Т1,Нм
Т1
=
 (8)
(8)
Т1
=
 Нм
Нм
- ведущего вала редуктора Т2,Нм
Т2
=
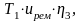 (9)
(9)
Т2
= 66∙4,6 0,96=291,5 Нм
0,96=291,5 Нм
- ведомого вала редуктора Т3,Нм
Т3
=
 (10)
(10)
Т3 = 291,5∙5∙0,98∙0,992∙0,98=1372 Нм

1.2 Расчёт зубчатой передачи редуктора.
Так
как в задании нет особых требований в
отношении габаритов передачи, принимаем
для зубчатых колес материал со средними
механическими характеристиками – сталь
45 с твердостью НВ < 350, термообработка
– улучшение. Для улучшения прирабатываемости
колес принимаем твердость по Бринеллю
для шестерни HB1
= 280, для колеса HB2
= 250[1]. Предел прочности материала колес
 ,
предел текучести
,
предел текучести
 [1].
[1].
Допускаемые
контактные напряжения для шестерни[ н1]
и колеса
н1]
и колеса
[ н2] ,МПа определим по формулам
 [
н1]
=
[
н1]
=
 ,
[
н2]
=
,
[
н2]
=
 ,
(11)
,
(11)
где [SН] - коэффициент безопасности , [SН] =1,1
KHL - коэффициент долговечности при числе циклов нагружения больше базового. При длительной эксплуатации редуктора KHL= 1
 предел
контактной выносливости при базовом
числе циклов нагружения,
МПа
предел
контактной выносливости при базовом
числе циклов нагружения,
МПа
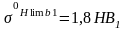 ,
,
 (12)
(12)
 ,
,
 МПа
МПа
Полученные
значения подставляем в формулу 11
[
н1]
=
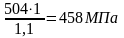 ,
[
н2]
=
,
[
н2]
=
Расчётное допускаемое контактное напряжение, [ н] , МПа, определяем по соотношению
[ н] =0,45 ( [ н1] + [ н2] ) , (13)
[ н] =0,45(458+409)=390,5 МПа.
Проверим выполнимость условия
[
н]
 1,23
[
н
]mi
n
1,23
[
н
]mi
n
390,5 1,23·409
Условие выполняется
Проверим выполнимость условия
[ н] 1,23 [ н ]mi n
490,5 1,23·518
Условие выполняется
Определяем межосевое расстояние передачи, aω, мм, из условия контактной выносливости активных поверхностей зубьев по формуле
a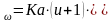
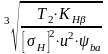 (14)
(14)
Принимаем
коэффициент, учитывающий неравномерность
распределения нагрузки между зубьями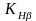 ,
,
 [1].
[1].
Принимаем
коэффициент
ширины венца по межосевому расстоянию
для косозубой передачи
 ba;
ba
=0,4[1].
ba;
ba
=0,4[1].
Принимаем коэффициент Ка для косозубых передач, Ка =43[1].
 a
a
Полученное значение округляем до стандартного большего[1].
Принимаем aω=200мм
Нормальный модуль зацепления принимаем по следующей
рекомендации
mn
≈(0,01…0,02)
 (15)
(15)
mn =(0,01…0,02)200=2,0…4,0мм
Согласовав с ГОСТ 9563-60 [1], примем mn =3,0 мм
Примем
предварительно угол наклона зубьев
 100
и определим числа зубьев шестерни и
колес:
100
и определим числа зубьев шестерни и
колес:
Z1=
Z1=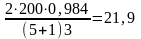 (16)
(16)
Принимаем целое число Z1=22,
Определяем число зубьев колеса Z2
Z2= =22·5=110
(17)
=22·5=110
(17)
Уточняем
значение угла наклона зубьев ,град
,град
cos
=
 (18)
(18)
cos
=
 Тогда
=80
Тогда
=80
Определяем делительные диаметры шестерни d1 и колеса d2, мм
d1
=
 , d2
=
, d2
=
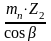 (19)
(19)
d1= ,
d2
=
,
d2
=
Проверяем межосевое расстояние aω, мм
а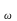 =
= (20)
(20)
а
=
Определяем диаметры вершин зубьев шестерни, dа1 , мм и колеса, dа2 , мм, по формуле
dа1 = d1 + 2m n , da2 = d 2 +2m n (21)
dа1=66,67+2·3=72,67мм , da2=333,33+2·3=339,33 мм
Определяем диаметры впадин зубьев, df1 , мм и колеса, df2 , мм, по формуле
df1 = d1 - 2,5m n , df2 = d 2 -2,5m n (22)
df1=66,67-2,5·3=59,17 мм , df2=333,33-2,5·3=325,83 мм
Определяем ширину колеса b2, мм
b2
=
 = 0,4·200=80 мм (23)
= 0,4·200=80 мм (23)
Ширина шестерни b1, мм
b1 = b 2 + 5 =80+5=85 мм (24)
Вычисляем коэффициент ширины шестерни по диаметру ψbd по формуле
 (25)
(25)

Окружную скорость колёс v, м/с, определяем по формуле
v
=
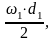 (26)
(26)
где ω1 - угловая скорость ведущего вала редуктора, рад/с; ω1=22 рад/с
d1- делительный диаметр шестерни, м; d1=0,067м
v= =0,8м/с
=0,8м/с
При полученной скорости v=0,8 м/с для косозубых передач принимаем 9 степень точности [1].
Определяем расчётные контактные напряжения , н , МПа, по формуле
н
= (27)
(27)
где aω -межосевое расстояние передачи, мм; aω =200мм.
Т2 – момент на ведомом валу редуктора, Нмм; Т2=1371∙103 Нмм.
b2- ширина колеса, мм; b2=80мм.

u – передаточное число редуктора; u=5.
КН - коэффициент нагрузки, определяемый по формуле
Кн
=
 (28)
(28)
где
KH –
коэффициент неравномерности нагрузки
по длине зуба; КHβ=1,04[1].
–
коэффициент неравномерности нагрузки
по длине зуба; КHβ=1,04[1].
KHV –коэффициент динамичности нагрузки, KHV =1,1[1].
KH –
коэффициент неравномерности распределения
нагрузки между
–
коэффициент неравномерности распределения
нагрузки между
зубьями
;  KH
=1,0[1].
KH
=1,0[1].
Кн
=
 =1,04·1,1·1,0=1,144
=1,04·1,1·1,0=1,144
Подставляем значения в формулу 27
н
=
Проверяем контактное напряжение
н
=515МПа>[ н]
=490МПа
н]
=490МПа
Условие прочности не выполнено.
Вычислим перегрузку П , % , по формуле
 (29)
(29)
Где σН- расчётное контактное напряжение, МПа; σН=515 МПа.
[σН] – допускаемое контактное напряжение, МПа; [σН] =490МПа.
 П=
П= %
%
Перегрузка 9%, следовательно, результаты расчёта можно признать удовлетворительными.
Определяем силы, действующие в зацеплении.
Окружную силу Ft, Н, вычисляем по формуле
Ft
=
 (30)
(30)
Где d1 – делительный диаметр шестерни, м; d1=0,067м
Т1 – момент на ведущем валу редуктора, Нм; Т1 = 291,5Нм
Ft
=
Радиальную силу Fr, Н, вычисляем по формуле
Fr
= Ft
 (31)
(31)
Где αω – угол зацепления; αω=20º.
β- угол наклона зубьев, β=8º.
Fr=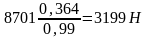
Осевую силу Fа, Н, вычисляем по формуле
Fa
= Ft
 (32)
(32)
Fa =8701·0,14=1223 Н
Проверяем зубья на выносливость по напряжениям изгиба. Вычисляем расчётное напряжение изгиба F, МПа, по формуле
F
=
 (33)
(33)
где Ft, - окружная сила, Н; Ft =2234Н
b2 - ширина колеса, мм; b2= 64 мм
mn – модуль зацепления, мм; mn=2,5мм
КF - коэффициент нагрузки вычисляем по формуле
КF = KF KFV (34)
где KF - коэффициент неравномерности распределения нагрузки по длине зуба; KF =1,1[1].
КFV - коэффициент динамичности КFV =1,1[1].
КF =1,1*1,1=1,21
Y - коэффициент, учитывающий компенсацию погрешности при использовании формулы для прямозубых передач
Y
= 1 -
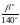 (35)
(35)
где β – угол наклона зубьев, град; β = 12,5º.
β=1-
КF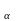 -
коэффициент, учитывающий неравномерность
распределения нагрузки между зубьями;
KF
-
коэффициент, учитывающий неравномерность
распределения нагрузки между зубьями;
KF
YF - коэффициент, учитывающий форму зуба зависит от эквивалентных чисел зубьев шестерни и колеса.
Эквивалентное число зубьев колеса и шестерни вычисляем по формулам
 ZV1
=
ZV1
=
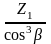 ZV2
=
ZV2
=
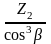 (36)
(36)
где z1 и z2 –числа зубьев шестерни и колеса; z1=22, z2 =110
ZV1
=
 ZV2
=
ZV2
=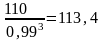
По вычисленным значениям выбираем коэффициенты YF1 и YF2
YF1=3,90, YF2=3,60
Выбираем из таблицы [1] коэффициент, учитывающий нестабильность свойств материала [SF]' =1,75 Коэффициент, учитывающий способ получения заготовки зубчатого колеса [S F]''=1
Вычисляем коэффициент безопасности по формуле
[S F]= [S F]' [S F]'' (37)
[S F]= =1,75·1=1,75
Вычисляем предел выносливости при отнулевом цикле изгиба 0Flim b1 и 0Flim b2 , МПа по формулам
0Flim b1=1,8НВ1 0Flim b1=1,8НВ2 (38)
0Flim b1=1,8·280=504 МПа; 0Flim b2=1,8НВ2·250=450 МПа
Определяем допускаемые напряжения для шестерни[ F1] ,МПа и
колеса[ F2], МПа, по формуле
[
F1]
=
 [
F2]
=
[
F2]
=
 (39)
(39)
[
F1]
=
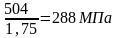 [
F2]
=
=
[
F2]
=
=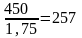
Определяем для шестерни и колеса отношения
 =
=
 =
= (40)
(40)
Дальнейший расчёт проводим для колёса, т. к. для него это отношение меньше. Расчётное напряжение изгиба F, МПа вычисляем по формуле 33
F
=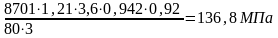
Расчётное напряжение изгиба F =136,8 МПа [ F]=257 МПа.
Условие прочности на изгиб выполнено.
1.3 Проектировочный расчёт валов редуктора
Проектировочный расчёт проводим на кручение по пониженным допускаемым напряжениям.
1.3.1 Ведущий вал
Диаметр
выходного конца d
в1
, мм при допускаемом напряжении
 =
25 МПа определяем по формуле
=
25 МПа определяем по формуле
d
в1
=
 (41)
(41)
где Т1- момент на ведущем валу, Нмм; Т1= 291,5 ∙103Нмм.
d
в1
=

Примем d в1 по ближайшему значению из стандартного ряда; d в1=40мм.
Диаметр вала под подшипниками dп1, мм принимаем из приблизительного расчёта с условием, что его величина должна быть кратна 5:
dп1 ≈ dв1 + 2t (42)
где t =2,5 мм.
dп1 ≈ 40+2·2,5=45мм
Диаметр переходного участка вала без колеса dбп1 вычисляем и принимаем по стандартному ряду, приведённому выше из приблизительного расчёта по формуле
dбп1 ≈ dп1 + 3,2r (43)
где r =3
dбп1=45+3,2·3=55мм
1.3.3 Ведомый вал
Учитывая
влияние изгиба вала от натяжения ремня,
принимаем [ к
] = 20 МПа.
к
] = 20 МПа.
Диаметр выходного конца вала d в2 , мм, определяем по формуле
dв2
=
 (44)
(44)
где Т2- момент на ведомом валу, Нмм; Т2= 1371 ∙103Нмм.
d
в2
=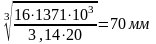
Диаметр под подшипниками, dп2 , мм, определяем по формуле
dп2 ≈ dв2 + 2t, (45)
где t =3,3 мм.
dп2=70+2·3,3≈75мм
Диаметр вала без колеса, dбп2 , мм, определяем по формуле
dбп2 ≈ dп2 + 3,2r, (46)
dбп2=75+3,2·3,5=85мм
Диаметр вала под колесом dк2 , мм, определяем по формуле
dк2 ≈ dбп2 +5мм (47)
dк2=85+5=90мм

