8. Система нерівностей
Нерівність
вигляду
розв’язується з допомогою побудови
графіка рівняння
.
Приклад. Знайти область існування функції
.
Величина
існує, якщо виконана система нерівностей
.
Будуємо
графіки рівнянь
,
і знаходимо
область, де виконано дві нерівності.
Якщо нерівність строго, то границя
позначається пунктирами. (Рис. 5). Шукана
область штрихується.
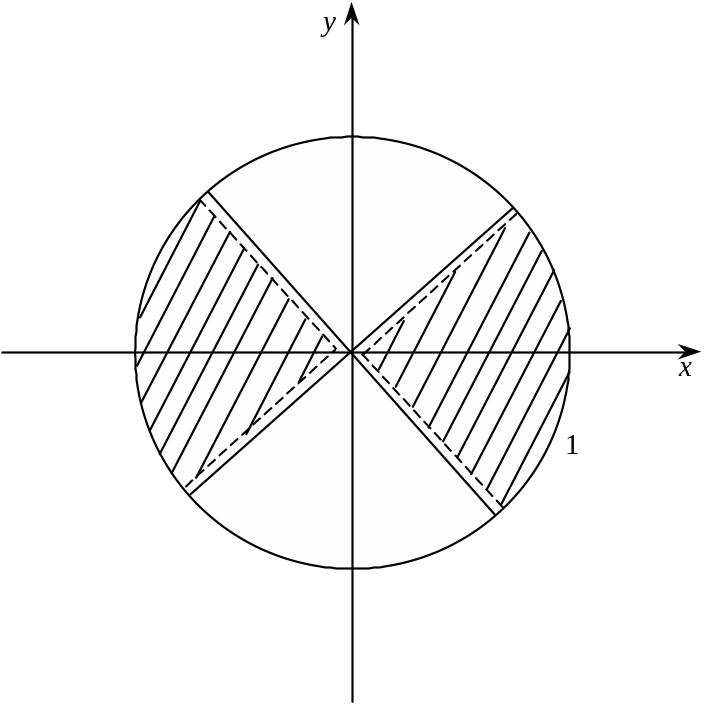
Рис. 5.
Приклад. Знайти область існування функції
.
Функція існує, якщо виконано нерівність
.
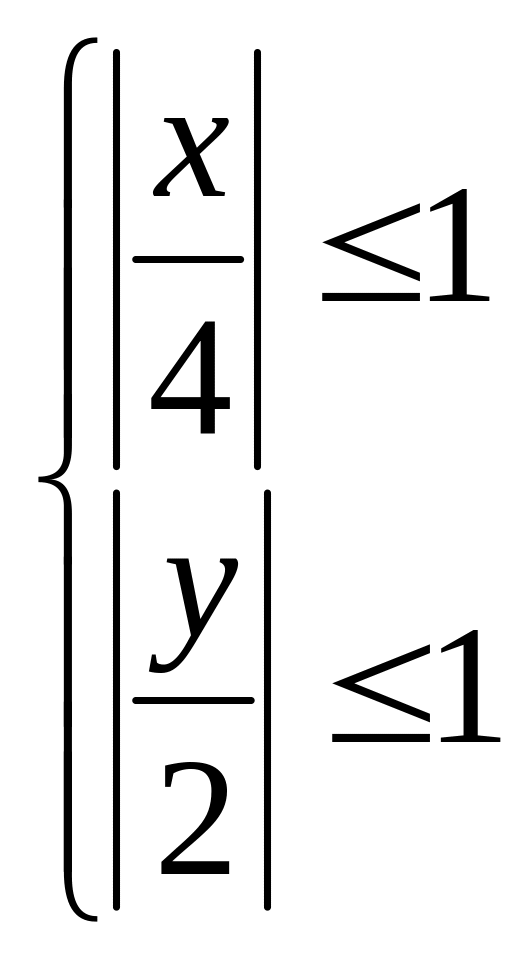
Область зображена на рис. 6
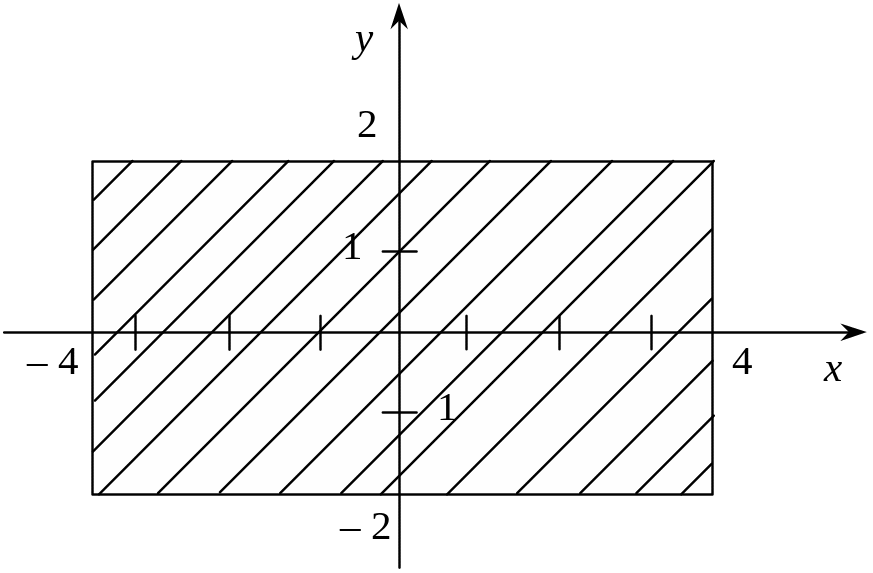
Рис. 6
9. Тригонометричні нерівності
Всі тригонометричні нерівності зводяться до одного з наступних нерівностей.
І.
.
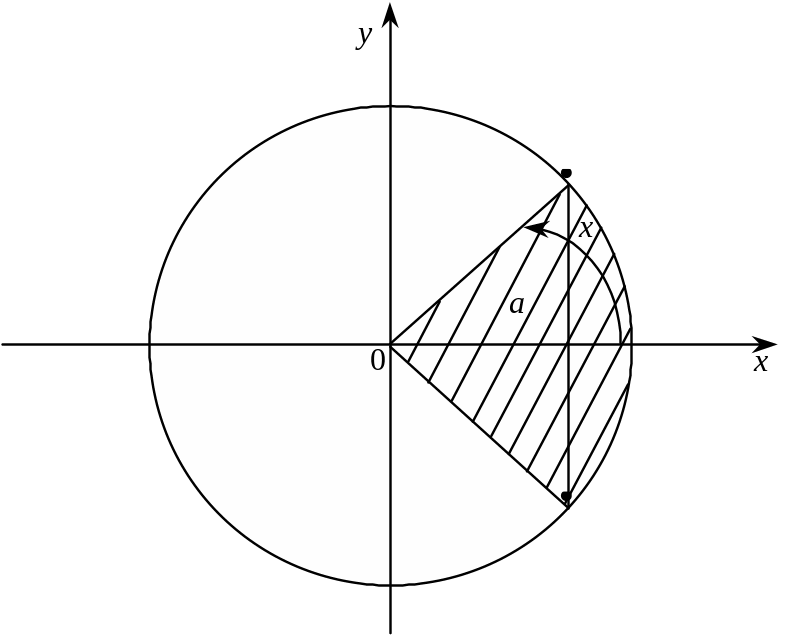
Рис. 7.
З рис. 7 знаходимо розв’язок
. (7)
Приклад. Розв’яжемо нерівність
.
Вважаючи
отримаємо квадратну нерівність
.
Розв’яжемо
нерівність
.
ІІ.
З рис. 7 знаходимо розв’язок
. (8)
Приклад. Розв’яжемо нерівність
.
Думаючи
,
отримаємо квадратну нерівність
.
Розв’яжемо нерівності
1)
;
2)
.
ІІІ.
.
Рис. 8
З рис. 8 знаходимо розв’язок нерівності
(9)
Приклад. Розв’яжемо нерівність
.
Покладемо
і розв’яжемо нерівність
.
Розв’яжемо нерівності
1)
;
2)
.
IV
.
З рис. 8 знаходимо розв’язок
(10)
Приклад. Розв’яжемо нерівність
.
Позначивши , приходимо до нерівності
.
Розв’яжемо нерівності
1)
;
2)
.
.
V.
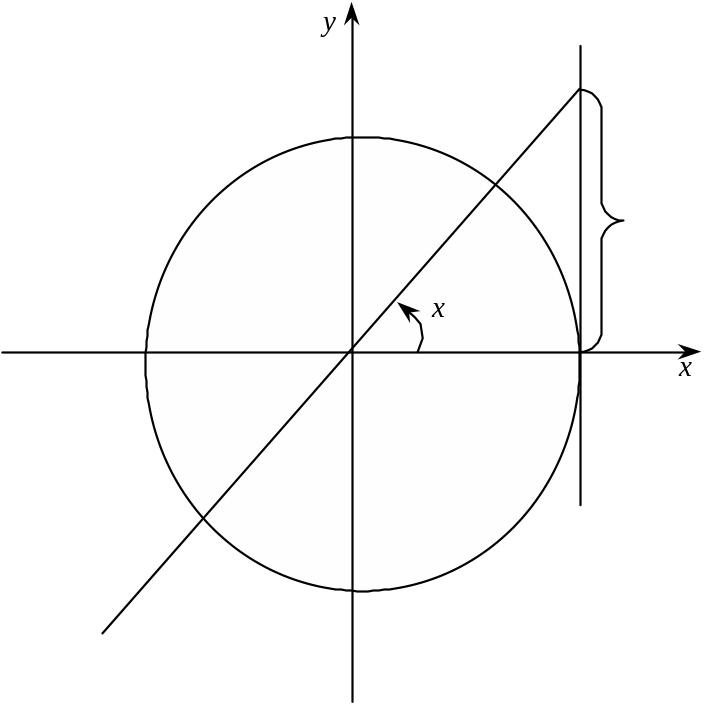
Рис. 9
З рис. 9 знаходимо розв’язок нерівності
. (11)
Аналогічно розв’язується нерівність
. (12)
Приклад. Розв’яжемо нерівність
.
Покладемо
.
Отримаємо нерівність
.
Розв’яжемо
нерівності:
.
VI
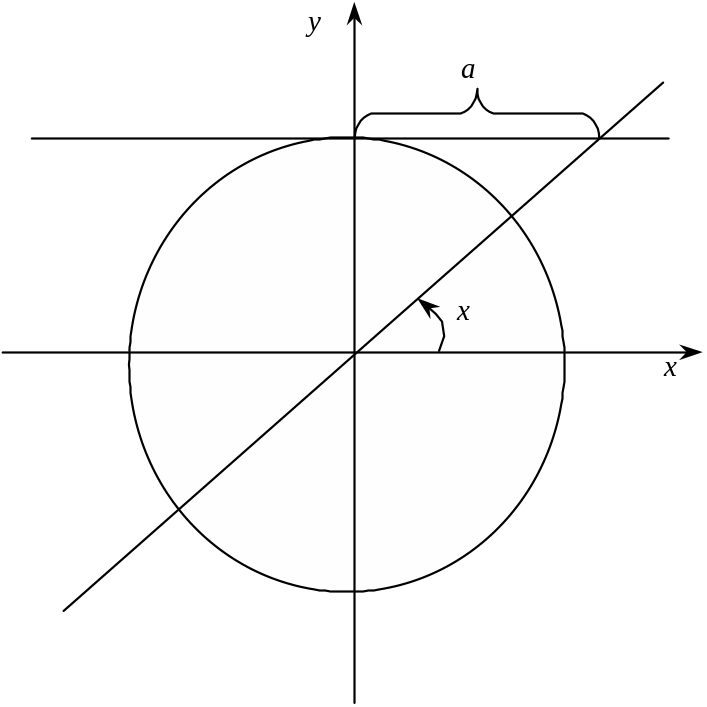
Рис. 10
Нерівність має розв’язок
(13)
Аналогічно
нерівність
має розв’язок
(13)
Приклад. Розв’яжемо нерівність
.
Думаючи
отримаємо
.
Розв’яжемо
нерівність,
.
Приклад. Розв’яжемо нерівність
.
Позначаючи
,
отримаємо нерівність
.
Розв’яжемо нерівність:
1)
;
2)
.
10. Алгебраїчні нерівності
Приведемо деякі невідомі нерівності
1. Нерівність Коші:
. (15)
2.
Нерівність Гельдера при
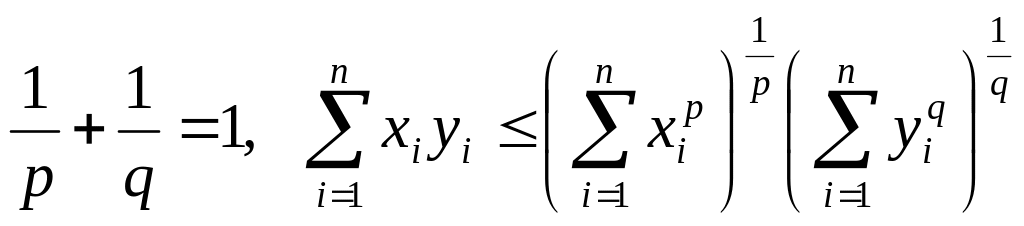. (16)
3.
(17)
Приведемо приклади розв’язку нерівностей.
Приклад. Довести нерівність
.
Якщо
,
то нерівність виконується. Якщо
,
то зведемо нерівність до квадратів
,
.
Нерівність виконано.
Приклад.
Довести, що для будь-якого трикутника
із сторонами
виконується нерівність
.
Оскільки дві частини нерівностей позитивні, то зведемо нерівність в квадрат
.
Оскільки
,
то нерівність виконано.
Приклад. Доказати нерівність
.
Помножимо нерівність на 2. Отримаємо нерівність
,
які очевидно виконуються.
Приклад. Довести, що при будь-яких додатних значеннях а і b має місце нерівність
.
Зведемо нерівність в квадрат
,
,
.
При тотожних перетвореннях нерівностей отримали здійснені нерівності, що доказує справедливість нерівності.
Приклад.
Довести, що
,
якщо
.
Покладемо
і розглянемо функцію
.
Щоб знайти мінімум функції
знаходимо похідну
.
З
рівняння
знаходимо
.
Отже
,
,
.
Якщо
,
то
.
Приклад. Довести нерівність
.
Розкриваючи дужки, отримаємо нерівність
,
,
.
При тотожних перетвореннях отримаємо очевидно виконану нерівність.