5. Пример. Растяжение ступенчатого стержня

Поясним основные понятия МКЭ на простейшем примере осевого растяжения ступенчатого стержня. Данный пример сейчас будет приведен лишь в качестве иллюстрации, без подробных объяснений.

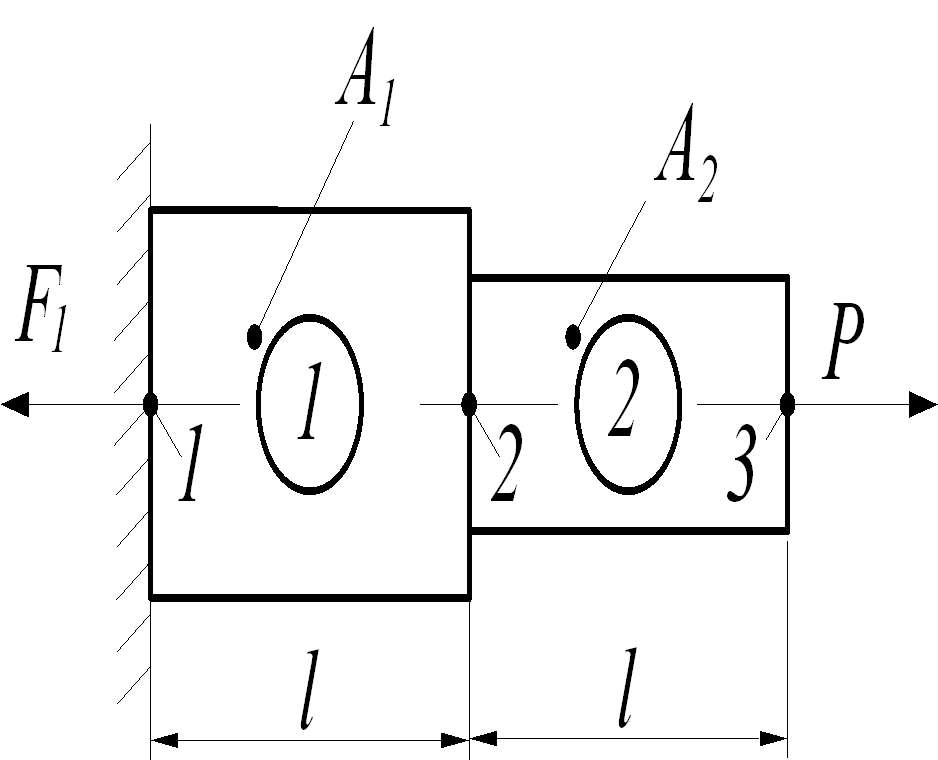
Рисунок 28 – Ступенчатый стержень

Ступенчатый стержень (Рисунок 28) с двумя ступенями одинаковой длины l и площадью поперечного сечения ступеней А₁ и А₂ жестко заделан с левого торца и нагружен на противоположном торце осевым усилием Р. Определить перемещения сечений 1, 2 и 3.

Разобьем стержень на два элемента (участка) 1, 2 и введем на границах элементов узлы 1, 2, 3, в которых будем отыскивать неизвестные перемещения u. Таким образом, ступенчатый стержень будем моделировать двумя последовательно соединенными стержневыми конечными элементами.

Рассмотрим отдельно стержневой элемент, изображенный на рисунке 29.

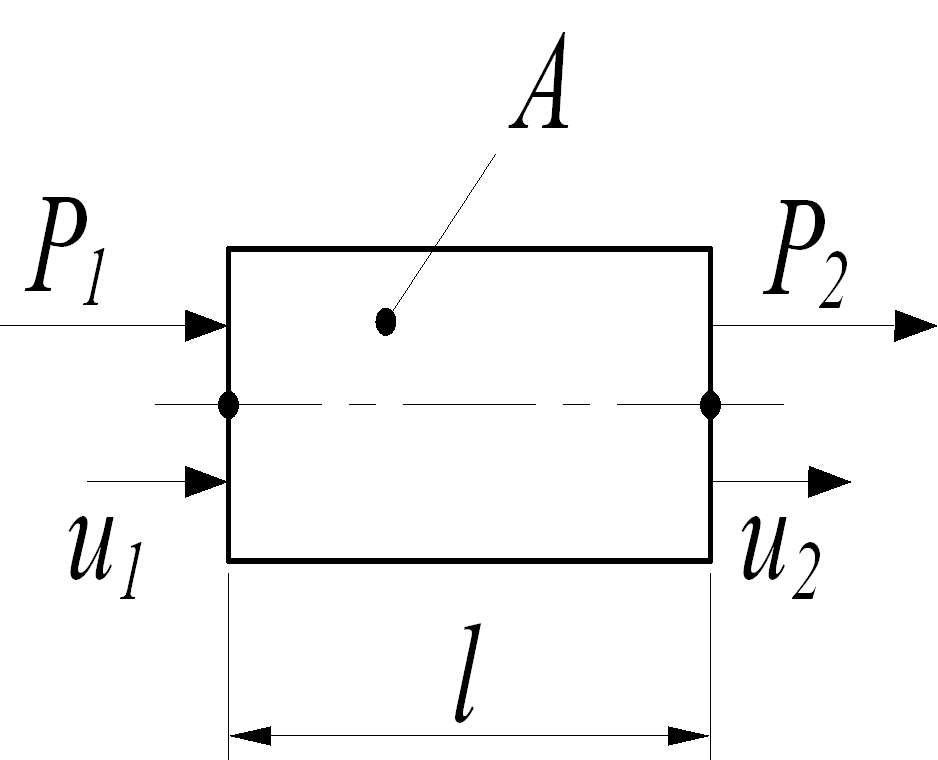
Рисунок 29 – Стержневой элемент

Он имеет длину l, площадь поперечного сечения А, в узлах приложены усилия Р₁ и Р₂, от которых эти узлы имеют осевые перемещения u₁ и u₂. Запишем для элемента на рисунке 29 соотношения, очевидные из курса сопротивления материалов:

, 1.1

или то же в матричной форме:

1.2

где Е – модуль упругости материала стержня.

Матрица , связывающая между собой в 1.2 узловые усилия и перемещения, носит название матрицы жесткости элемента.

Составим уравнение равновесия для всего стрежня, изображенного на рисунке 28, объединив соотношения для элементов 1 и 2, записанные с учетом (1.2). Так как стержень состоит из нескольких элементов, то естественно предположить, что матрица жесткости всего стержня должна включать в себя матрицы жесткости образующих его элементов. Для данной задачи главные диагонали матриц жесткости элементов должны совпадать с главной диагональю глобальной (общей) матрицы жесткости всего стержня и состыковываться в узле 2 (Рисунок 28).

На основании (1.2) общую систему уравнений равновесия можно записать в виде:

,

или

1.3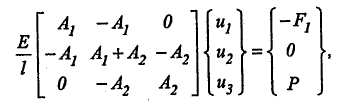

где u_i – перемещение i-го узла всей системы. В (1.3) учтено, что усилие Р приложено в узле 3, а усилие F₁ (реакция опоры) – в узле 1. Узел 2 свободен от внешних нагрузок.

Теперь следует наложить граничные условия в перемещениях, а именно: u₁=0. Это достигается замещением 1-й строки и 1-го столбца нулями и помещением на главную диагональ любого числа, отличного от нуля:

Решением этой системы линейных алгебраических уравнений является:

1.4

2Основные идеи метода конечных элементов

Метод конечных элементов (МКЭ) – это способ анализа поведения реальной конструкции при заданных нагрузках и перемещениях. Основной единицей представления конструкции в этом анализе является конечный элемент (КЭ) – геометрически упрощенное представление малой части физической конструкции. Модель конструкции создается при помощи конечных элементов.

МКЭ – один из основных способов, применяемых для решения задач строительной механики, механики деформируемого твердого тела, теплопроводности, гидромеханики и др. Идея метода заключается в аппроксимации сплошной среды с бесконечным числом степеней свободы совокупностью простых элементов, имеющих конечное число степеней свободы и связанных между собой в узловых точках.

Для МКЭ характерны: широкий диапазон применимости, инвариантность по отношению к геометрии конструкции и механическим характеристикам материалов, простота учета взаимодействия конструкций с внешней средой (механические и температурные нагрузки, граничные условия и т.д.), высокая степень приспособленности к автоматизации всех этапов расчета. Популярность метода объясняется также простотой его физической интерпретации и очевидной связью с методами Ритца и перемещений, широко применяемыми в механике сплошных сред и строительной механике.

Основы МКЭ были разработаны различными специалистами - математиками, физиками и инженерами, а сам термин конечный элемент появился в статье Клаффа, посвященной решению плоской задачи теории упругости [1].

Конечные элементы (КЭ) объединяются в модель в некоторых точках пространства, называемых узлами. В этих точках элементы соединяются и движутся совместно. Узлы, которые пронумерованы для того, чтобы их можно было отличить друг от друга, вместе с элементами осуществляют приближенное геометрическое описание сложной модели. В зависимости от типа, ориентации и числа элементов, соединяющихся в узле, последний может противодействовать поступательным перемещениям и вращениям вдоль и относительно определенных направлений. Каждое отдельное возможное перемещение или вращение называется степенью свободы и представляет собой неизвестную величину, подлежащую определению. Таким образом, перемещение узла определяется его поступательными перемещениями вдоль глобальных осей координат X, У и Z и его вращениями относительно этих осей (т.е. узел может иметь всего 6 степеней свободы).

Созданная для расчета конечно-элементная модель – всего лишь приближенное представление реальной конструкции. Как во всех численных методах, расчет производится не для реальной конструкции, а для построенного упрощенного образа, т.е. модели. Таким образом, точность результатов конечно-элементного анализа зависит от качества разработанной модели.

В настоящее время возможности МКЭ значительно расширены [3] ‑ [5] что, несомненно, обусловлено появлением современных высокопроизводительных ЭВМ и программных комплексов, реализующих МКЭ.

Основное уравнение (система уравнений) МКЭ для решения задач статического нагружения имеет вид:

[К]*{d}={F},

где [К] – глобальная матрица жесткости исследуемой конструкции;

{F} – вектор приложенных статических нагрузок (сосредоточенных и распределенных);

{d} – вектор узловых перемещений исследуемой конструкции.

Система уравнений может быть решена относительно неизвестных, в качестве которых выступают узловые перемещения (линейные и угловые).

После определения узловых перемещений во всех узлах исследуемой конструкции и вычисления линейных и угловых деформаций находят напряжения, действующие в узлах конструкции, используя закон Гука.

Определив эквивалентные напряжения, на основании выбранной гипотезы прочности делают вывод о том, обеспечивается прочность исследуемой конструкции или нет, выявляются зоны концентрации напряжений (концентраторы) и слабонагруженные участки (зоны) конструкции.

Расчет с помощью метода конечных элементов в форме метода перемещений включает следующие этапы:

• разбиение конструкции на конечные элементы и подготовка топологической, геометрической и физической информации, установление факторов взаимодействия с окружающей средой;

• построение для выделенных конечных элементов соответствующих матриц жесткости и векторов, определяющих зависимости между реакциями и перемещениями в узлах элемента;

• формирование разрешающей системы линейных алгебраических уравнений;

• решение полученной системы уравнений и установление полей перемещений, внутренних силовых факторов и т.д.;

• обработку результирующей информации и ее анализ.

Перечисленные этапы поддаются четкой универсальной алгоритмизации, и их программная реализация не вызывает принципиальных затруднений при наличии библиотеки стандартных подпрограмм, реализующих второй, третий и четвертый этапы расчета.

В данном учебном пособии рассматриваются вопросы, связанные с применением метода конечных элементов для решения задач статического нагружения исследуемых конструкций, описываемых системой уравнений .