Точность результатов
Численный анализ, к которому относится и МКЭ, требует некоторой идеализации реальной конструкции. Поэтому, несмотря на мощное развитие вычислительной техники, результаты вычислений по МКЭ не свободны от ошибок. Использование вычислительной техники в роли «черного ящика», без понимания основных процессов и этапов вычислений, может привести к существенным ошибкам. К сожалению, не исключены также и ошибки операторов.
Приступая к конечно-элементному анализу, инженер должен понять:
К какой области анализа относится данная задача;
Какая часть всей конструкции должна исследоваться подробнее;
Какие упрощения можно допустить в данной задаче.
Естественно, это требует определенной квалификации исследователя.
Ошибки могут возникать на различных стадиях конечно-элементного анализа: при постановке задачи, дискретизации (построении модели), численном решении.
Ошибки постановки задачи могут возникать, когда выбранный тип конечных элементов или их размер не соответствует физическому поведению материала в конструкции. Несколько уменьшить эту ошибку (по крайней мере, ту ее часть, которая связана с размером конечного элемента) можно, используя автоматическое построение сетки. Однако основным источником ошибок при постановке задачи является некорректное задание граничных условий. Таким образом, успех конечно-элементного анализа зависит от точности воспроизведения на модели граничных условий, геометрии и свойств материала натурной конструкции.
Ошибки дискретизации возникают при замене реальной конструкции ограниченным числом конечных элементов (с учетом их формы и размеров).
Ошибки, связанные с численным решением систем уравнений, обычно менее значимы, чем перечисленные выше два типа ошибок.
При
конечно-элементном анализе, как правило,
неизвестными являются смещения, и
результатом решения в этом случае будет
вектор смещений в узле
.
Смещения в других точках элемента
вычисляются интерполяцией.
После аппроксимации поля смещений (в пределах элемента) соответствующим полиномом, называемым «функцией формы», могут быть вычислены деформации и напряжения. Описанная схема вычислений показывает, что наибольшая точность достигается при определении смещений в узлах.
Деформации вычисляются дифференцированием соответствующих смещений, поэтому максимальная точность вычислений деформаций и напряжений будет в центре элемента. На рисунке 24 показана деформированная частица для случая чистого изгиба.
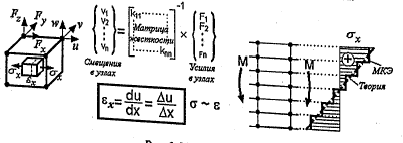
Рисунок 24 – Деформированная частица для случая чистого изгиба
Как видим, теоретическое и численное решение совпадает в центральной части конечного элемента.
Тип и количество элементов влияют на точность вычислений. Так, например, при вычислении силы в случае нелинейного анализа, при небольшом числе конечных элементов их количество существенно влияет на величину вычисляемой силы (Рисунок 25). Однако при увеличении числа элементов результаты стабилизируются.
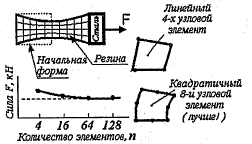
Рисунок 25 – Зависимость типа КЭ от величины вычисляемой силы
Существует два метода конечно-элементного анализа: h-метод (h – длина стороны КЭ) и р-метод (р – порядок полинома аппроксимирующей функции). Для повышения точности решения h-метод требует увеличения числа элементов. В соответствии с р-методом для увеличения точности надо повысить порядок полинома аппроксимирующей функции. Так, например, на рисунке 26 элементы более высокого порядка демонстрируют и большую точность результатов по сравнению с линейными элементами (Рисунок 26 а).
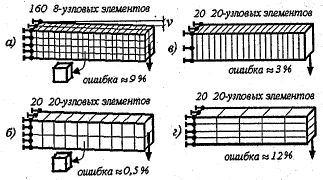
Рисунок 26 – Зависимость результата от количества числа элементов
На точность результатов влияет также и ориентация сторон элементов. Для изгибаемой консольной балки увеличение числа элементов по высоте балки не дает повышения точности результатов (Рисунок 26 в). Гораздо лучшие результаты дает увеличение числа элементов второго порядка по длине балки (Рисунок 26 г).
Для получения достоверных результатов в зонах концентрации напряжений размер элементов должен быть меньше. На рисунке 27 показан фрагмент растягиваемой полосы с центральным отверстием. Известно, что максимальные напряжения действуют в сечении А-А, поэтому в окрестности данного сечения сетка элементов должна быть гуще, чем у левой границы полосы.
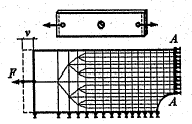
Рисунок 27 – Фрагмент растягиваемой полосы с центральным отверстием