Граничные условия
Задание граничных условий – один из ответственных этапов конечно-элементного анализа. Так, например, на модели (Рисунок 17), изображенные графические граничные условия в узлах А и В служат для того, чтобы перемещение указанных узлов модели соответствовали перемещениям тех же узлов натурной конструкции с учетом наложенных на них связями ограничений. При этом перемещения могут приобретать как нулевые (в узле А), так и не нулевые (в узде В) значения. Существуют также граничные условия, при которых задаются нагрузки (узел С).
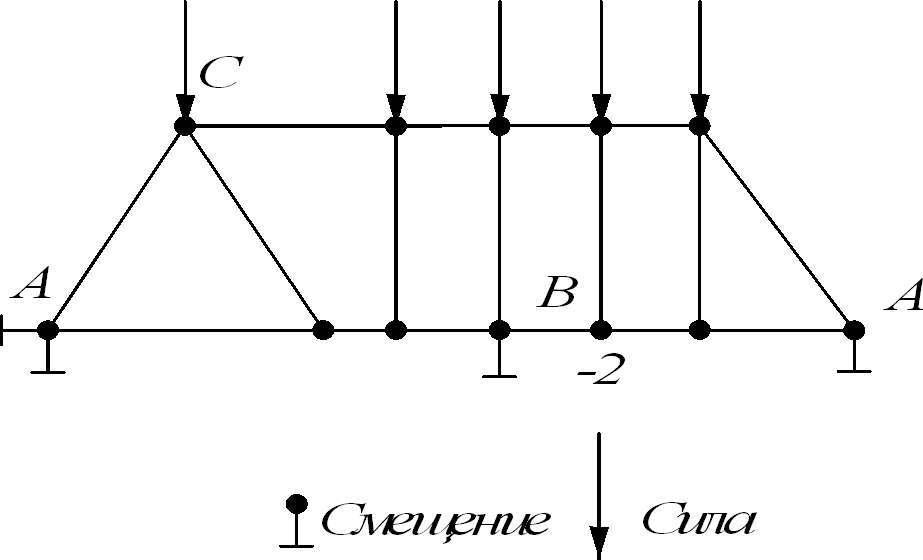
Рисунок 17 – Граничные условия
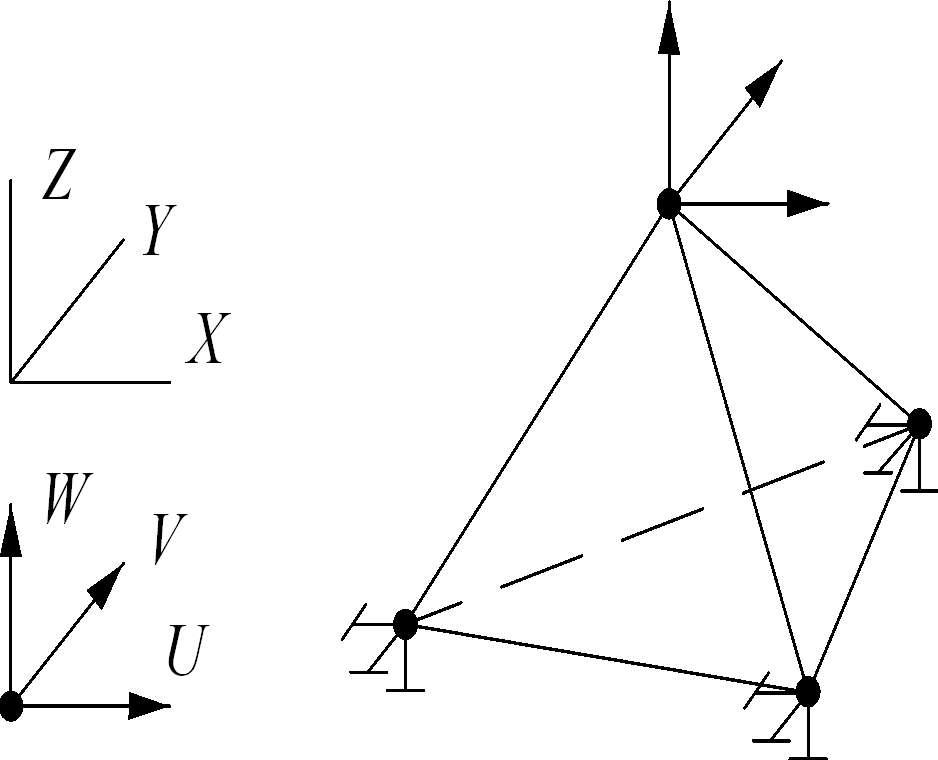
Рисунок 18 – Приложение граничных условий
Граничные условия (перемещения или силы) прикладываются только к узлам (Рисунок 18). Максимальное число граничных условий, приложенных в узле, равно числу его степеней свободы – 3 силы или 3 перемещения.
Необходимо обратить особое внимание на то, что число граничных условий должно быть минимально необходимым (не меньше и не больше). Так, например, не следует фиксировать все степени свободы (все перемещения) в каждом узле элемента (Рисунок 19 а); не следует также прикладывать силу в узле в том же самом направлении, в котором в данном узле зафиксировано смещение (Рисунок 19 б); полное отсутствие закрепления вдоль какой-либо из осей (Рисунок 19 в) может привести при анализе к кажущемуся сдвигу вдоль этой оси вследствие неизбежных ошибок округления при численных расчетах. Для рассмотренных примеров правильные схемы граничных условий смотри Рисунок 19 (г, д).
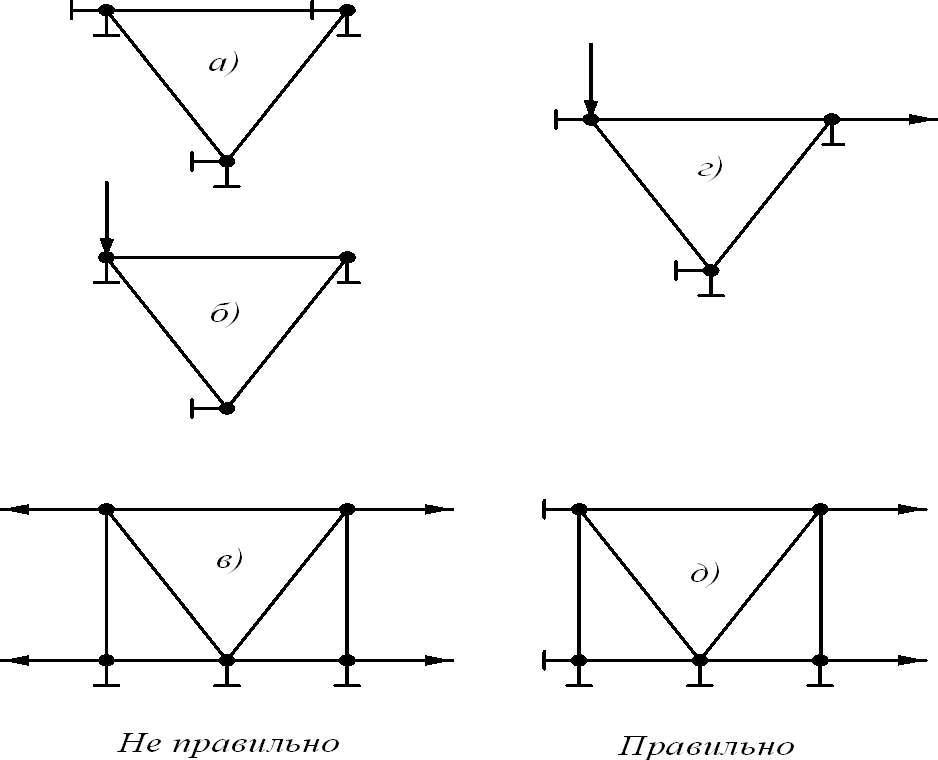
Рисунок 19 – Число граничных условий
Схема размещения граничных условий зависит от вида нагружения (растяжение, чистый изгиб, сдвиг), смотри .
Рисунок 20 – Схема размещения граничных условий
Если конструкция имеет оси или плоскости симметрии, то при назначении граничных условий необходимо это учитывать. Так, например, пресс с жесткими пуансонами, сжимающий куб из более мягкого однородного материала (Рисунок 21), имеет три плоскости симметрии. Очевидно, в этом случае нет необходимости моделировать всю конструкцию целиком.
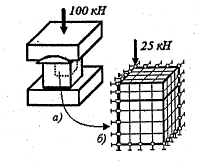
Рисунок 21 – Пресс с жесткими пуансонами
Можно смоделировать только часть конструкции (1/4 или 1/8), имея в виду, что в точках на плоскостях симметрии соответствующие перемещения равны нулю. Это обстоятельство мы учитываем соответствующими граничными условиями в узлах элементов, лежащих на плоскостях симметрии (Рисунок 21б).
Выбор размеров элементов и граничных условий при построении сетки можно существенно упростить, если принять во внимание принцип Сен-Венана: две статически эквивалентные системы сил создают одно и тоже поле напряжений на расстоянии от их точек приложения, больше, чем характерный линейный размер поперечного сечения (b>a, Рисунок 22).
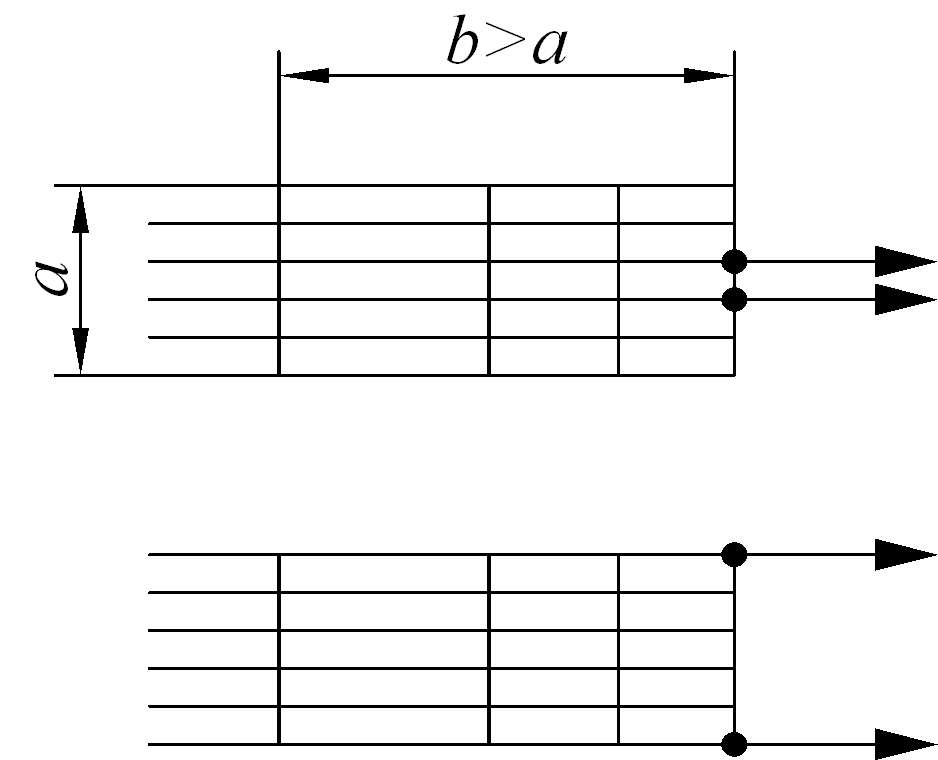
Рисунок 22 – Принцип Сен-Венана
Рассмотрим следующую ситуацию. Известно, что чрезмерно большие растягивающие напряжения являются основной причиной многих разрушений. В этом случае, если зона максимальных растягивающих напряжений находится вдали от точки приложения силы (например, как на схеме Рисунок 23), нет
Рисунок 23 – Расчетный случай
необходимости строить подробную сетку элементов вблизи этой точки, т.к. здесь действуют, в основном, сжимающие напряжения.