
- •Ответы на вопросы второго коллоквиума по дисциплине «Системы управления»
- •Необходимость и значение автоматизации производства в химической промышленности
- •Технологический объект управления, его входные и выходные величины
- •Понятие о нормальном технологическом режиме
- •Задачи управления
- •Системы автоматизации
- •Местный контроль и ручное управление
- •Дистанционный контроль
- •Системы автоматического регулирования (аср)
- •Структурная схема аср
- •Характеристика отдельных элементов
- •Понятие об объектах регулирования (ор)
- •Объекты с сосредоточенными и распределенными параметрами
- •Управляемые и управляющие величины объектов
- •Статические и динамические режимы ор
- •Уравнения статики и динамики; статические и динамические характеристики
- •Линеаризация нелинейных характеристик
- •Чувствительность информационных каналов ор
- •Задачи, решаемые с использованием статических и динамических характеристик
- •Самовыравнивание как свойство объектов регулирования
- •Степень самовыравнивания. Ее влияние на вид динамической характеристики объекта
- •Устойчивые и нейтральные объекты
- •Емкость как свойство ор и характеристика инерционных свойств ор
- •Время разгона
- •Влияние емкости на вид динамической характеристики ор Одно-, двух- и многоемкостные объекты
- •Запаздывание как свойство ор. Время запаздывания
- •У равнения динамики и динамические характеристики устойчивых и нейтральных объектов с запаздыванием
- •Уравнения динамики и динамические характеристики объектов регулирования 1-го и 2-го порядка
- •Связь между структурой уравнения динамики объекта и его свойствами. Пример
- •Аналитическое определение свойств ор
- •Состав математической модели ор
- •Модели статики и динамики
- •Последовательность составления уравнений динамики ор
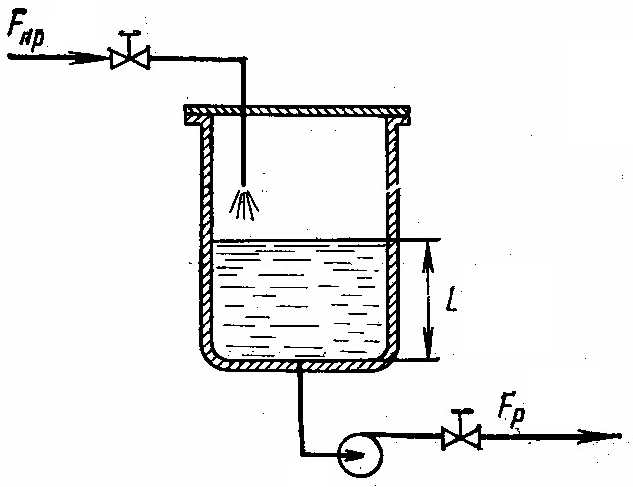
- •Составление уравнения динамики и нахождение динамической характеристики гидравлического резервуара со свободным сливом жидкости
- •Составление уравнения динамики и нахождение динамической характеристики гидравлического резервуара, жидкость из которого откачивается центробежным насосом
- •Экспериментальное определение свойств ор
- •Пример определения свойств объекта по кривой разгона
- •Аппроксимация объектов второго порядка
- •Автоматические регуляторы (ар). Определение
- •Структурная схема
- •Классификация ар по наличию и виду подводимой энергии, регулируемой величине, характеру действия, характеру регулирующего воздействия, закону регулирования
- •Позиционные регуляторы. Их особенности
- •Статическая и динамическая характеристики
- •Переходный процесс и критерии качества регулирования в системах с позиционными регуляторами
- •Работа пи-регулятора в замкнутом контуре
- •Работа пид-регуляторов в замкнутом контуре
- •Преимущества и недостатки, область применения
- •Исполнительные устройства
- •Исполнительные механизмы и регулирующие органы. Их виды
- •Составление уравнения динамики и нахождение переходной характеристики аср, состоящей из устойчивого объекта регулирования 1-го порядка без запаздывания и п-регулятора
- •Составление уравнения динамики и нахождение переходной характеристики аср, состоящей из устойчивого объекта регулирования 1-го порядка без запаздывания и пд-регулятора
- •Составление уравнения динамики и нахождение переходной характеристики аср, состоящей из устойчивого объекта регулирования 1-го порядка без запаздывания и пи-регулятора
- •Типовые динамические звенья
- •Уравнения динамики, переходные характеристики, передаточные функции звеньев
- •Изображение приборов и средств автоматизации на функциональных схемах.
- •Основные условные обозначения
- •Регулируемые величины и функциональные признаки приборов
- •Примеры
- •Развернутый и упрощенный варианты построения условных графических обозначений систем регулирования
- •Автоматизация центробежных и поршневых насосов и компрессоров
- •Цель автоматизации насосов
- •Составить и обосновать схему регулирования указанных объектов управления
- •Цель автоматизации компрессоров
- •Составить и обосновать схему регулирования указанных объектов управления
- •29 Автоматизация теплообменников смешения и поверхностных теплообменников
- •Технологический объект управления – выпарная установка. Сформулировать цель автоматизации
- •Составить и обосновать схему регулирования основных технологических переменных, используя одноконтурные аср.
- •Технологический объект управления – барабанная прямоточная сушилка, в которой сушильным агентом являются топочные газы
- •Сформулировать цель автоматизации
- •Составить и обосновать схему регулирования основных технологических переменных, используя одноконтурные аср
- •Технологический объект управления – ректификационная установка
- •Составить и обосновать схему регулирования основных технологических переменных, если целевым продуктом является дистиллят, используя одноконтурные аср
- •Технологический объект управления – ректификационная установка
- •Составить и обосновать схему регулирования основных технологических переменных, если целевым продуктом является кубовая жидкость, используя одноконтурные аср
- •Технологический объект управления – абсорбционная установка
- •Составить и обосновать схему регулирования основных технологических переменных, если целевым продуктом является обедненный газ, используя одноконтурные аср
- •Технологический объект управления – абсорбционная установка
- •Составить и обосновать схему регулирования основных технологических переменных, если целевым продуктом является насыщенный абсорбент, используя одноконтурные аср
Запаздывание как свойство ор. Время запаздывания
Запаздывание объекта выражается в том, что его выходная величина начинает изменяться не сразу после нанесения возмущения, а только через некоторый промежуток времени τ, называемый временем запаздывания. Все реальные объекты обладают запаздыванием, так как изменение потоков вещества или тепла распространяется в объектах с конечной скоростью и требуется время для прохождения сигнала от места, где фиксируется изменение выходной величины. Обозначив это расстояние через l, а скорость прохождения сигнала через s, выразим время запаздывания следующим образом:
τ = l / s.
У равнения динамики и динамические характеристики устойчивых и нейтральных объектов с запаздыванием
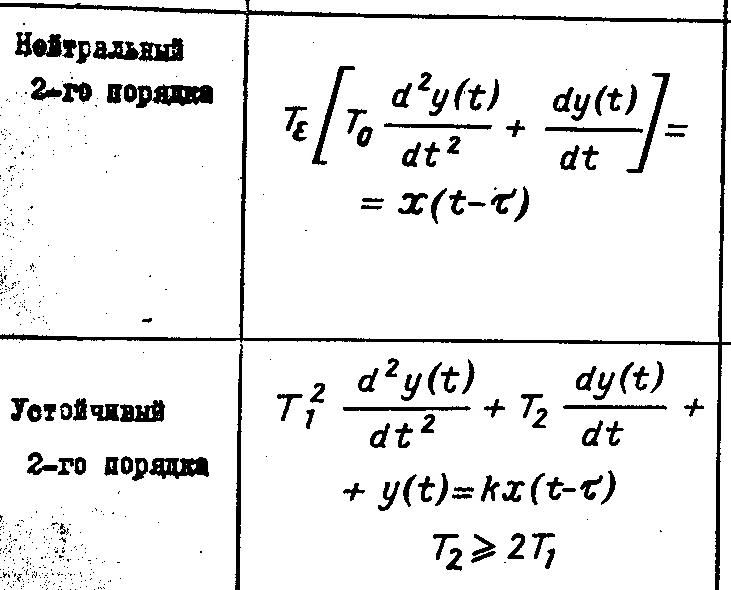
Уравнения динамики и динамические характеристики объектов регулирования 1-го и 2-го порядка
В зависимости от вида дифференциального
уравнения динамики реального объекта
химической технологии целесообразно
различать объекты первого, второго и
высокого порядков.
зависимости от вида дифференциального
уравнения динамики реального объекта
химической технологии целесообразно
различать объекты первого, второго и
высокого порядков.
Связь между структурой уравнения динамики объекта и его свойствами. Пример
Поведение большинства объектов химической технологии по конкретному каналу, например каналу x-y, может быть аппроксимировано уравнением динамики вида
Т∙(dy(t) / dt) + y(t) = k∙x∙(t-τ).
Наличие слагаемого «+ у» в левой части уравнения свидетельствует о том, что в объекте имеется внутренняя отрицательная обратная связь, он устойчив и обладает положительным самовыравниванием, величина которого обратна коэффициенту усиления. Отсутствие такого слагаемого указывает на отсутствие в объекте обратной связи; такой объект нейтрален. Если слагаемое «у» имеет отрицательный знак, то в объекте существет внутренняя положительная обратная связь и он неустойчив.
Количество емкостей в объекте определяется порядком старшей производной. В нашем случае объект имеет одну емкость, величина которой определяется отношением Т/k.
Запаздывание определяют по наличию времени запаздывания τ в аргументе слагаемого правой части уравнения.
Таким образом, рассматриваемый объект по каналу x-y является устойчивым одноемкостным объектом с запаздыванием.
Аналитическое определение свойств ор
Аналитический метод заключается в составлении математического описания объекта, при котором находят уравнения статики и динамики на основе теоретического анализа физических и химических процессов, протекающих в исследуемом объекте, и с учетом конструкции аппаратуры и характеристик перерабатываемых веществ. При выводе этих уравнений используются фундаментальные законы сохранения веществ и энергии, а также кинетические закономерности процессов химических превращений, переноса тепла и массы.
Аналитический метод применяют при проектировании новых технологических объектов, физико-химические процессы которых достаточно хорошо изучены. Он позволяет прогнозировать работу объектов в статическом и динамическом режимах, однако сопряжен с трудностью решения и анализа составленных уравнений и требует проведения специальных исследований для определения численных значений коэффициентов этих уравнений. Кроме того, точность математического описания реальных объектов в большой степени зависит от введения упрощающих допущений.
