Санкт-Петербургский государственный политехнический университет

Факультет технической кибернетики

Кафедра компьютерных систем и программных технологий

Отчёт по расчетному заданию №3

Марковские модели принятия решений

по курсу

Методы оптимизации

Работу выполнил студент группы № 5081/12 Бойцев Андрей Сергеевич

Работу принял преподаватель ________ Сиднев Александр Георгиевич

Санкт-Петербург

2012

Задание Вариант №1

Фирма ежегодно оценивает положение со сбытом своей продукции как удовлетворительное (состояние S₁) или не­удовлетворительное (состояние S₂). Необходимо принять решение о целесообразности рекламирования продукции c целью расширения ее сбыта при конечном (N=3) и бесконечном горизонтах планирования, если приведенные ниже матрицы Р₁ и Р₂ определяют переходные ве­роятности рассматриваемой системы при наличии рекламы (допустимое решение X₁) и без нее (допустимое решение X₂) в течение любого года, а соответ­ствующие им доходы заданы матрицами R₁ и R₂.

При решении задачи планирования воспользуйтесь:

в случае конечного горизонта

1. методом полного перебора;

2. методом итераций по стратегиям;

в случае бесконечного горизонта планирования

1. Методом полного перебора;

2. методом итераций по стратегиям;

3. методами линейного программирования.

1. Решение задачи в случае конечного горизонта планирования

1. Метод итераций по стратегиям

Данную задачу можно представить как задачу динамического программиро­вания (ДП) с конечным числом этапов, следующим образом.

Пусть число состояний для каждого этапа (года) равно т (2 в данном примере). Обозначим через f_i(j) оптимальный ожидаемый доход, полученный на этапах от i до N включительно.

Оптимальный ожидаемый доход fi(j) на этапах с номерами i, i+1, …, N складывается из 2-х составляющих – оптимальный ожидаемый доход на (i+1)-м этапе

Вторая составляющая оптимального ожидаемого дохода fi(j) определяется совокупностью оптимальных ожидаемых доходов fi+1(k):

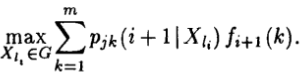
В результате приходим к рекуррентному уравнению динамического программирования с конечным числом этапов:

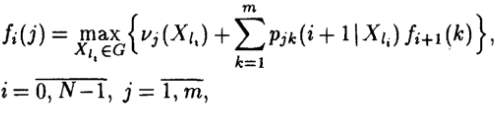
Воспользовавшись матрицами P1, P2, R1, R2 и их независимостью от номера этапа, вычислим ожидаемые доходы, при различных вариантах допустимых решений:

Воспользуемся табличным алгоритмом решения задачи(табл. 1.1.1 – этап 3, табл. 1.1.2 – этап 2, табл. 1.1.3 – этап 1).

Таблица 1.1.1

j			Оптимальный ожидаемый доход f3(j)	Оптимальное решение
	k=1	k=2
1	1,7	3,1	3,1	X2
2	-0,6	-0,4	-0,4	X2

Таблица 1.1.2

j			Оптимальный ожидаемый доход f2(j)	Оптимальное решение
	k=1	k=2
1	4,45	5,15	5,15	X2
2	1,10	-0,10	1,10	X1

Таблица 1.1.3

j			Оптимальный ожидаемый доход f1(j)	Оптимальное решение
	k=1	k=2
1	6,45	7,04	7,04	X2
2	2,93	1,51	2,93	X1

Из оптимального решения следует, что в первые два года необходимо использовать рекламу лишь в случае неудовлетворительного положения со сбытом, а в третий год не использовать.