2.4. Особенности искривленной поверхности раздела фаз

Остановимся еще на одном очень важном качестве дисперсных систем, связанном с раздробленностью, — резком увеличении кривизны поверхности частиц по сравнению с плоскостью. За счет кривизны поверхности жидкой дисперсной фазы возникает избыточное внутреннее давление Δр (рис. 2.6). Равнодействующая сил поверхностного натяжения σ как векторная величина компенсируется силой Δр, которая направлена к центру частицы и перпендикулярна ее поверхности. В результате совершается работа dW, которая приводит к уменьшению объема тела на величину dV. Эта работа

dW = Δр∙dV, (2.21)

где Δр – избыточное внутреннее давление.

Изменение поверхностной энергии можно выразить через энергию Гиббса [см. уравнение (2.1)] или через энергию Гельмгольца [см. уравнение (2.4)]. В условиях равновесия (dF = 0) и постоянства других параметров (dТ = 0, dn_i = 0, dq = 0) с учетом соотношения (2.21) можно записать

0 = – ΔрdV + σdB, или Δр = σ(dB/dV). (2.22)

Величина dB/dV – кривизна поверхности, в случае сферических частиц она обратна радиусу этих частиц, т.е. dB/dV = ±2/r (знак «–» соответствует вогнутой поверхности, знак «+» — выпуклой). С учетом этого, а также соотношения (1.6) можно записать

Δр = ±2σ/r = ±4σD, (2.23)

где D – дисперсность, м^–1.

С увеличением дисперсности внутреннее давление в капле воды при 5° С и приращение свободной энергии Гиббса в расчете на один моль воды [см уравнение (2.25)] изменяются следующим образом:

Диаметр частиц а, м(мкм)	10–4 (100)	10–6 (1)	10–8(0,01)
Дисперсность D, м–1	104	106	108
Внутреннее давление, Δр, МПа	3∙10–3	3∙10–1	3∙10
Приращение энергии Гиббса ΔGМ, кДж/моль	0,164	16,4	1,64∙103

Проведенные на основе формулы (2.23) расчеты показывают, что чем меньше размеры капель и выше поверхностное натяжение, тем интенсивнее внутреннее давление, а форма капель ближе к сферической даже в условиях гравитационного поля Земли. Форма небольших капель росы и относительно крупных капель ртути служит тому подтверждением

Соотношение (2.23) имеет для коллоидной химии принципиальное значение, оно позволяет объяснить повышенную реакционную способность раздробленной фазы, одну из особенностей дисперсных систем.

Вернемся еще раз к уравнению (2.1). При условии, что dT = 0, dB = 0, dn_i = 0 и dq = 0, для индивидуальных веществ, когда V = V_М (V_М – мольный объем), получим

dG_М = V_Мdp, или ΔG_М = V_МΔp. (2.24)

Если воспользоваться уравнением (2.23), то из формулы (2.24) можно получить следующее выражение:

ΔG_М = ± 2σV_М/r = ± 4DσV_М . (2.25)

П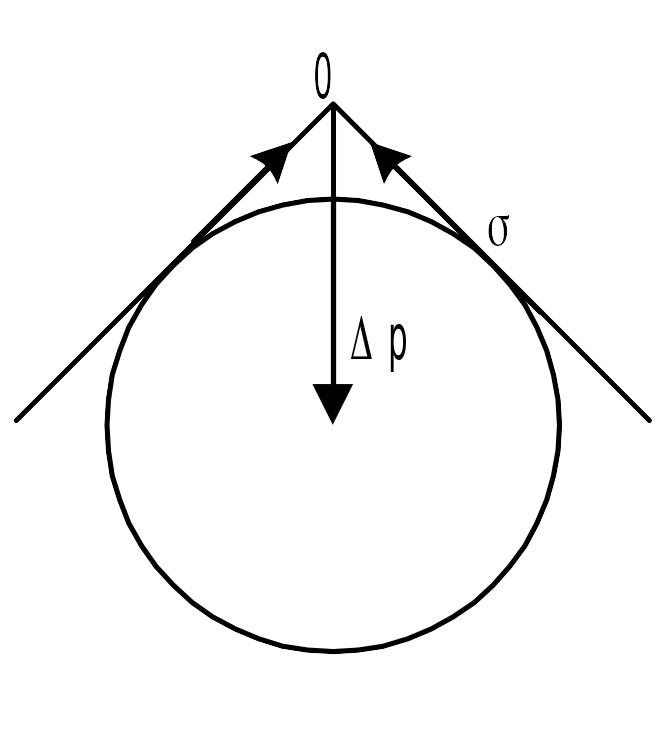 риращение энергии Гиббса в расчете на один моль вещества за счет кривизны поверхности, т.е. значения ΔG_М для капель воды различных размеров, приведены выше.

В

Рис. 2.6 Схема образования избыточного внутреннего давления Δp

еличина ΔG_М показывает, насколько увеличивается энергия Гиббса за счет кривизны выпуклой поверхности (знак «+») или в результате раздробленности дисперсной фазы. Иначе говоря, в результате раздробленности поверхность приобретает дополнительный избыток поверхностной энергии. Это обстоятельство существенным образом влияет на интенсификацию всех поверхностных явлений и создает дополнительные возможности для протекания самопроизвольных процессов.

Кроме того, кривизна поверхности влияет на давление насыщенного пара (рис. 2.7). Молекула А, находящаяся на плоской границе раздела фаз, испытывает воздействие соседних молекул; сфера действия межмолекулярных сил на рисунке заштрихована. На выпуклой поверхности это воздействие меньше, а на вогнутой – больше по сравнению с плоскостью. Поэтому переход молекул из жидкого состояния в парообразное на выпуклой поверхности (см. рис. 2.7,а) происходит легче: число молекул, необходимое для насыщения, достигается при меньшем давлении, а давление насыщенного пара больше по сравнению с таковым на плоской поверхности.

На вогнутых поверхностях (см. рис. 2.7,в) сфера взаимодействия поверхностных молекул с объемными увеличивается, переход в парообразное состояние затруднен, и поэтому давление насыщенного пара будет меньше, чем над плоской поверхностью.

Соотношение между давлением насыщенного пара над плоской и вогнутыми (или выпуклыми) поверхностями определяется уравнением Кельвина:

ln (p/p_S)= ± 2σ_ЖГ V_М/(rRT), (2.26)

где p_S, p – давление насыщенного пара над плоской и искривленными поверхностями соответственно; V_м — мольный объем жидкости; знак «+» относится к выпуклой, а знак «–» — к вогнутой поверхности; r — радиус кривизны.

Увеличение давления насыщенного пара тем значительнее, чем меньше радиус кривизны жидкости или размер капель: для капель диаметром 1 мкм оно составляет 0,1%, 100 нм – 1%, 10 нм – уже 10% по сравнению с плоской поверхностью.

Таким образом, значительная поверхность раздела фаз в сочетании с большим избытком поверхностной энергии и кривизной частиц дисперсной фазы приводит к тому, что возникают условия для самопроизвольного снижения поверхностной энергии на границе между дисперсной фазой и дисперсионной средой.

Раздробленность вещества влияет на кинетику, изменяя скорость физико-химических процессов на границе раздела фаз. На поверхности сахарной пыли, взвешенной в воздухе, настолько быстро идет процесс окисления, что достаточно небольшой искры для возникновения пламени, которое может послужить источником взрыва; такой же эффект наблюдается и в случае мучной пыли. Высокодисперсный порошок железа способен даже к самовозгоранию.

То, что в одних процессах является нежелательным (самовозгорание, взрыв) в других, наоборот, приносит пользу. Жидкое топливо (бензин, керосин, нефть, мазут) при работе двигателей внутреннего сгорания, дизелей, реактивных двигателей, котлов и других устройств дробится на капли, т.е. превращается в дисперсную систему, за счет чего достигается его более эффективное их использование. Для интенсификации различных процессов порошки переводят во взвешенное состояние. Этот процесс называют псевдоожижением. Образующийся кипящий слой позволяет «оголить» поверхность частиц и с большей эффективностью осуществить процесс, протекающий на границе раздела фаз.

Раздробленность позволяет полнее использовать вкусовые и пищевые свойства продуктов. Чтобы почувствовать аромат кофе, необходимо раздробить зерна и превратить продукт в дисперсную систему. Хлебопекарные свойства муки проявляются после дробления зерен (пшеницы или ржи) и образования дисперсной системы.

Итак, раздробленность оказывает существенное влияние на целый комплекс свойств: химические (окисление, горение, восстановление и др.); физические (испарение, конденсация, растворение); оптические; структурно-механические и прочностные; гидро- и аэродинамические, связанные с перемещением частиц совместно с жидкостью или газом; специфические (вкусовые, бактерицидные, дезинфицирующие) и многие другие.

Рис. 2.7. Изменение давления насыщенного пара (p_s) над выпуклой (а), плоской (б) и вогнутой (в) поверхностями (заштрихована сфера действия молекулярных сил)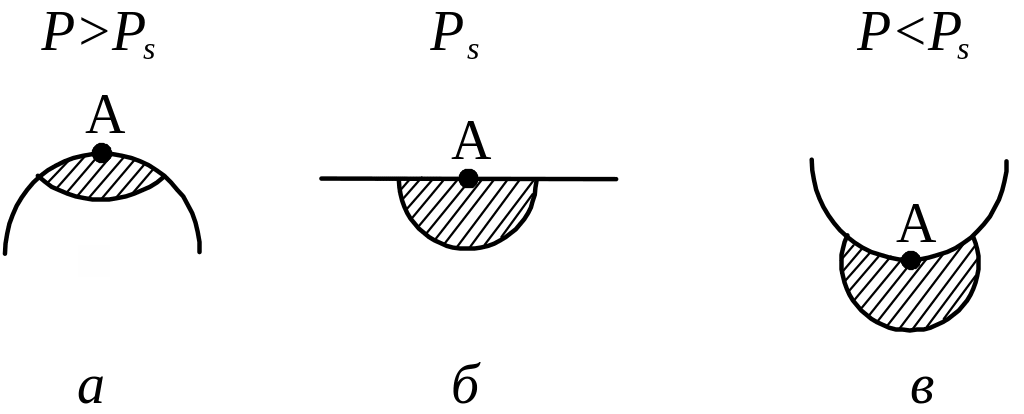

Приведенная на рис. 2.4 схема, с одной стороны, позволяет рассматривать энергетические аспекты дисперсных систем на базе фундаментальных представлений химической термодинамики, а с другой стороны, объединяет разнообразные поверхностные явления на основе общего подхода, связанного с энергией образования поверхности и с изменением этой энергии. В дальнейшем, по мере изучения курса, перечисленные в этой схеме явления рассматриваются более подробно.

Упражнение

Как увеличится свободная поверхностная энергия капель, содержащихся в 1 кг майонеза, по сравнению с нераздробленной его массой площадью 0,65 ∙ 10^–3 м² ? Чему равно внутреннее давление и приращение энергии Гиббса для капель жировой фракции майонеза диаметром 35 мкм? Плотность жировой фракции 0,9 ∙ 10³ кг/м²; межфазовое поверхностное натяжение 55 мДж/м²; мольный объем жира 0,19 м³/мoль.

Удельная поверхность капель майонеза согласно формуле (1.4) составляет

Поверхность капель увеличится по сравнению с поверхностью нераздробленной массы в n раз:

в соответствии с формулой (2.11) во столько же раз увеличится свободная поверхностная энергия.

Внутреннее давление находим по формуле (2.23):

Приращение энергии Гиббса за счет кривизны капель майонеза рассчитываем по формуле (2.25):

Г л а в а 3