1.3.2. Общие сведения о трапециевидных несущих поверхностях

П

а б

Рис. 1.7. Различные представления системы: корпус + несущая поверхность

ри рассмотрении несущей поверхности на корпусе (рис 1.7) обычно различают поверхность, составленную из консолей, находящихся в потоке (рис. 1.7, а), или поверхность с учётом так называемой подкорпусной части (рис. 1.7, б).

О

Рис. 1.8. Основные параметры трапециевидного крыла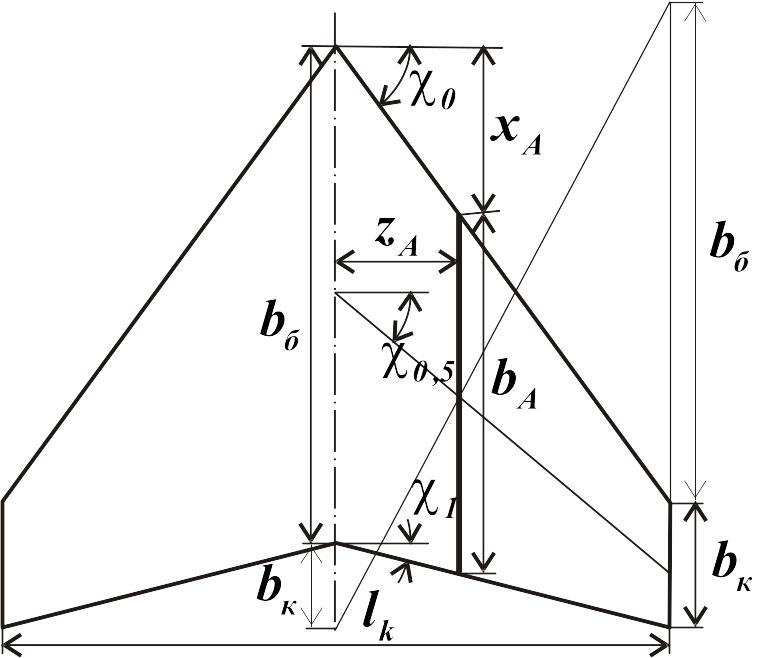

ба подхода имеют свои преимущества и недостатки. Основное отличие этих подходов состоит в использовании различных значений коэффициентов интерференции. Далее будет использоваться первый подход, т. е. будут рассматриваться только те части, которые находятся в потоке. В этом случае под несущими поверхностями будут рассматриваться поверхности, составленные из консолей, находящихся в потоке (рис. 1.7, а). Приведенные формулы могут быть использованы и для нахождения параметров несущих поверхностей с подкорпусной частью. Для этого необходимо в них подставлять соответствующие величины. Например, вместо подставлять , вместо – . Связь между основными параметрами этих несущих поверхностей приведена ниже.

Геометрия трапециевидной поверхности (рис. 1.8) характеризуется стреловидностью и тремя размерами: размахом или , центральной или бортовой и концевой хордами. По ним могут быть определены все другие параметры несущей поверхности.

Например, если она образована консолями, находящимися в потоке, то сужение , обратное сужение , площадь и удлинение определятся следующими формулами:

, ; (1.12)

; (1.13)

. (1.14)

Очень важными параметрами несущей поверхности являются углы стреловидности. При этом иногда необходимо знать угол стреловидности не только передней кромки, но также и задней или линии середин хорд. Зная угол стреловидности какой-либо линии крыла, можно найти аналогичное значении любой другой линии. Например, если заданы углы стреловидности передней ( ) и задней ( ) кромок, то угол стреловидности линии -хорд ( ) можно определить по формуле

. (1.15)

Если задан угол стреловидности только передней кромке, то тангенсы углов стреловидности линии -хорд, или задней кромки ( ), или линии середин хорд ( ) определяют по следующим формулам:

; (1.16)

; (1.17)

. (1.18)

Важнейшей геометрической величиной несущей поверхности, широко используемой при аэродинамических исследованиях, является её средняя аэродинамическая хорда, в качестве которой обычно понимают хорду эквивалентного крыла прямоугольной формы в плане, имеющего при той же площади почти такие же аэродинамические характеристики. Строго говоря, величина средней аэродинамической хорды и её координаты должны зависеть от геометрических характеристик несущей поверхности и от распределения аэродинамической нагрузки по хорде и размаху. Если предположить, что она распределена равномерно, то величина средней аэродинамической хорды и координата его носка определяют по таким формулам [16]:

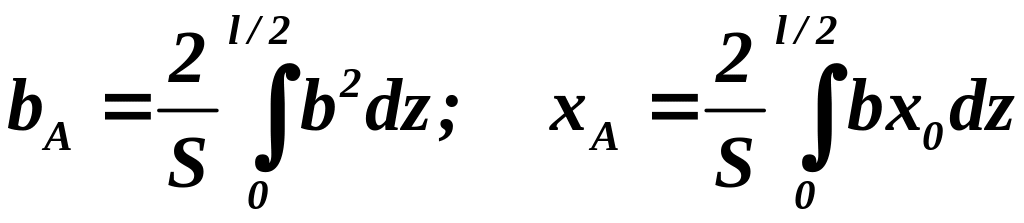. (1.19)

При этих предположениях координата середины средней аэродинамической хорды совпадает с центром тяжести площади несущей поверхности в плане. Следует заметить, что эти формулы используют для стандартного определения значения средней аэродинамической хорды и расстояния .

Для поверхности, состоящей из трапециевидных консолей, эти величины удобно определять по таким формулам:

; (1.20)

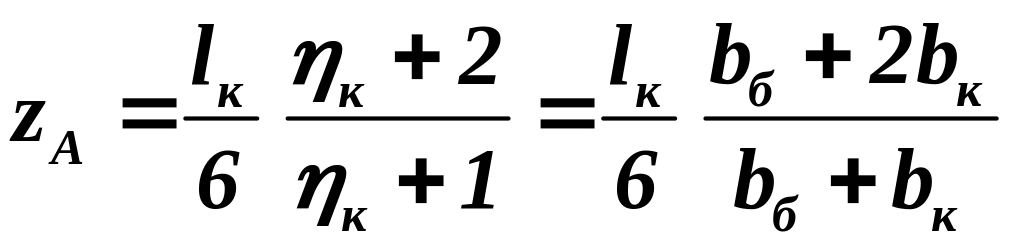; (1.21)

. (1.22)

На рис. 1.8 показан геометрический метод построения средней аэродинамической хорды для трапециевидных крыльев. Для этого необходимо продлить бортовую хорду на величину концевой, а концевую хорду с противоположной стороны – на величину бортовой. Соединить эти точки прямой. Пересечение этой прямой с линией середин хорд позволяет установить значение и «положение» средней аэродинамической хорды.

Довольно часто требуются основные параметры несущей поверхности с подкорпусной частью. Следует также учесть, что площадь несущей поверхности с подкорпусной частью иногда называют габаритной площадью, а в ряде случаев она принимается за характерную площадь для ЛА. Если соединение консолей с корпусом выполнено по схеме среднеплана, то для трапециевидных несущих поверхностей можно по известным параметрам несущей поверхности, составленной из находящихся в потоке консолей, определить аналогичные параметры для поверхности с подкорпусной частью:

; (1.23)

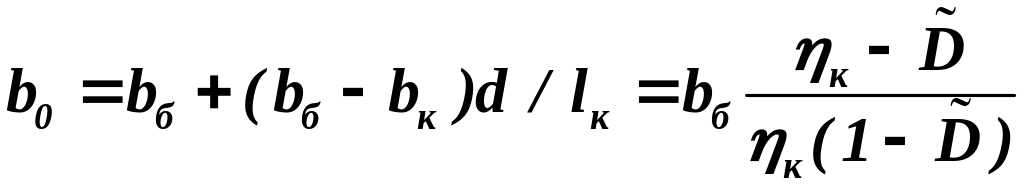; (1.24)

; (1.25)

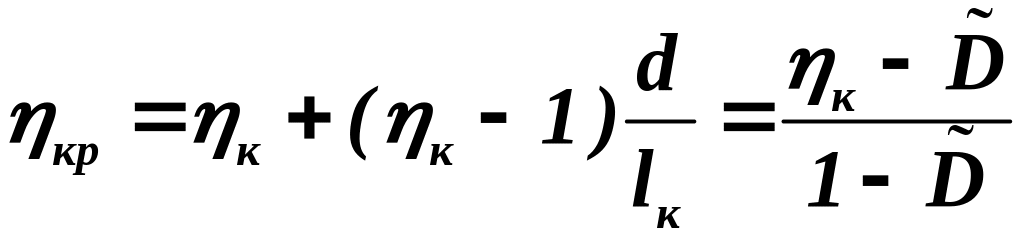; (1.26)

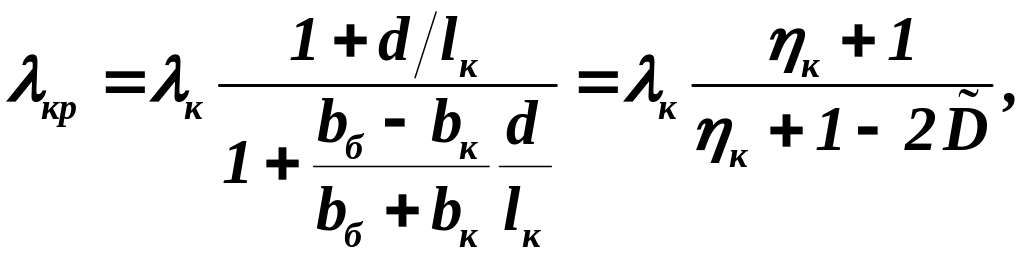(1.27)

где .

Выбор формы несущей поверхности в плане является одним из наиболее ответственных при разработке ЛА и должен быть основан на глубоких теоретических и экспериментальных исследованиях, учитывающих назначение ЛА и конкретные условия его полёта.