3.4. Интерференция корпуса и несущей поверхности

Рассмотрим физическую картину взаимодействия корпуса и несущей поверхности, полагая, что поверхность расположена на его цилиндрической части по схеме среднеплана.

Набегающий на тело поток можно представить как результат наложения друг на друга двух потоков: параллельного оси тела со скоростью и поперечного потока со скоростью . Рассматривая обтекание цилиндрической части тела поперечным потоком, можно прийти к выводу, что в точках, лежащих в месте предполагаемого размещения несущей поверхности, местные скорости потока больше, чем . Согласно теории потенциального обтекания цилиндра несжимаемой средой, поперечная скорость на этой линии определяется по выражению

,

где – расстояние от оси цилиндра. Если на корпусе в этой плоскости разместить несущую поверхность, то фактический угол атаки каждого её профиля будет переменным по размаху:

. (3.26)

В бортовом сечении угол атаки , а по мере удаления от него он уменьшается, приближаясь к значению угла атаки на бесконечности, т. е. к . Следовательно, подъёмная сила консолей, установленных на корпусе по схеме среднеплана, должна быть больше подъёмной силы аналогичных изолированных поверхностей.

Для учёта этого явления вводится коэффициент интерференции , определяемый как отношение дополнительной подъёмной силы, возникшей на консолях -й несущей поверхности при установке их на корпус, к подъёмной силе изолированной несущей поверхности. Например, для первых несущих поверхностей

. (3.27)

Консоли несущей поверхности, в свою очередь, оказывают воздействие на обтекание корпуса, так как давление на верхней и нижней поверхностях консолей передаётся на соответствующие участки корпуса. В результате такого воздействия на корпусе образуется дополнительная подъёмная сила, которая учитывается введением коэффициента интерференции . Например, для первых несущих поверхностей

. (3.28)

Часть корпуса, расположенная за несущей поверхностью, может попасть в зону влияния вихревой пелены, сходящей с поверхности, что вызовет уменьшение угла атаки на этом участке корпуса. Однако это влияние обычно оказывается не очень существенным.

Если с качественной стороны явление интерференции между корпусом и несущей поверхностью представляется более или менее ясным, то количественная оценка этого явления получается весьма сложной и пока недостаточно разработанной. В настоящее время имеются приближённые методы расчёта коэффициентов интерференции, основанные на различных допущениях, однако большая часть результатов получена по теории тонкого тела [3, 6].

Согласно теории тонкого тела коэффициенты интерференции между корпусом и несущей поверхностью, расположенной по схеме среднеплана, определяются только относительным диаметром корпуса ( – полный размах -й несущей поверхности, установленной на корпусе) и имеют такой вид:

; (3.29)

; (3.30)

. (3.31)

С

Рис. 3.5. Теоретические значения коэффициентов интерференции

ледует заметить, что формула (3.29) – точный результат, полученный по теории тонкого тела, а формулы (3.30) и (3.31) представляют собой приближённую аппроксимацию довольно громоздких выражений. На рис. 3.5 показаны графики этих зависимостей от относительного диаметра . На этом же графике штрихпунктирной линией показана изредка используемая зависимость .

Экспериментальными исследованиями установлено, что приведенные теоретические формулы дают наиболее достоверные результаты для несущей поверхности без сужения, т. е. при . У поверхностей с большая часть площади примыкает к корпусу, поэтому они испытывают более сильное интерференционное воздействие и в свою очередь значительнее влияют на обтекание корпуса. Указанное увеличение коэффициентов интерференции может быть учтено введением поправочного множителя . Обработка приведенных в работе [8] данных позволяет рекомендовать для его определения следующую формулу:

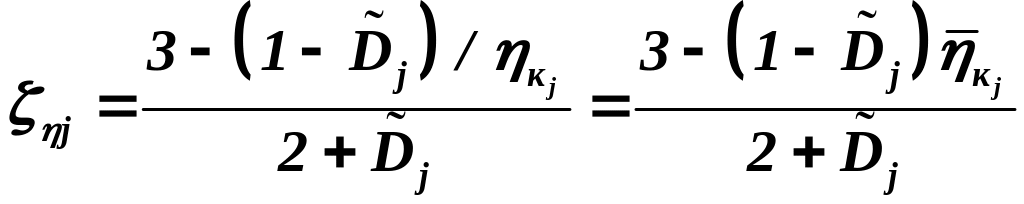. (3.32)

На рис. 3.5 пунктирными линиями показаны значения коэффициентов интерференции при .

Теоретические формулы для коэффициентов интерференции получены для несущих поверхностей, установленных на бесконечно длинном цилиндре. Установка несущих поверхностей вблизи носовой части корпуса приводит к уменьшению коэффициентов интерференции. Для учёта этого обстоятельства вводится поправочный коэффициент , приближённо определяемый по формуле [8]

(3.33)

в зависимости от параметра ( – расстояние от носика корпуса до середины бортовой хорды консоли: ).

Некоторые исследования [8] свидетельствуют о том, что на коэффициенты интерференции оказывает влияние вязкость среды. Это влияние выражается в увеличении эффективного радиуса корпуса на толщину вытеснения пограничного слоя, что приводит к увеличению коэффициентов интерференции. Это же приводит к уменьшению эффективной площади консолей, находящихся во внешнем потоке, что влечёт за собой уменьшение их подъёмной силы. Поэтому влиянием пограничного слоя на коэффициенты интерференции в большинстве случаев можно пренебречь.

Влияние числа на коэффициенты интерференции можно учесть введением поправочного множителя , который при дозвуковых скоростях принимается равным единице, а при может быть вычислен по формуле

. (3.34)

Ч

а б в г д

Рис. 3.6. Влияние консолей на корпус при сверхзвуковых скоростях для плоской конфигурации ЛА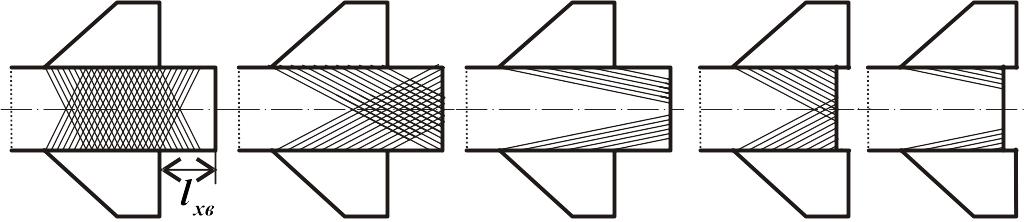

исло также оказывает существенное влияние на распределение дополнительной подъёмной силы, возникающей на корпусе (рис. 3.6). При дозвуковых и околозвуковых скоростях полёта зона влияния несущей поверхности на корпус в основном расположена между бортовыми хордами. Однако при сверхзвуковых скоростях возмущения от консолей распространяются вниз по потоку так, что зона влияния каждой консоли будет ограничена винтовыми линиями, выходящими от начала и конца бортовой хорды и пересекающими образующие корпуса под углом Маха. Смещение зоны влияния вниз по потоку будет тем сильнее, чем больше число . Это смещение сказывается на положении центра давления дополнительной подъёмной силы, индуцируемой поверхностью на корпусе, а иногда и на величину этой силы.

Если длина хвостовой части корпуса, расположенной за бортовой хордой несущей поверхности, достаточно велика, то можно считать, что эта сила реализуется полностью (рис. 3.6, а). Однако если несущая поверхность расположена вблизи донного среза, то эта сила полностью реализоваться не может и с ростом числа будет наблюдаться её уменьшение (рис. 3.6, б и в). Для учёта этого влияния вводится поправочный коэффициент , который при дозвуковых скоростях полёта равен единице.

Следует обратить внимание, что рисунок выполнен для более простой, так называемой плоской конфигурации.

П

Рис. 3.7. Влияние длины хвостовой части корпуса на величину дополнительной подъёмной силы и положение фокуса этой силы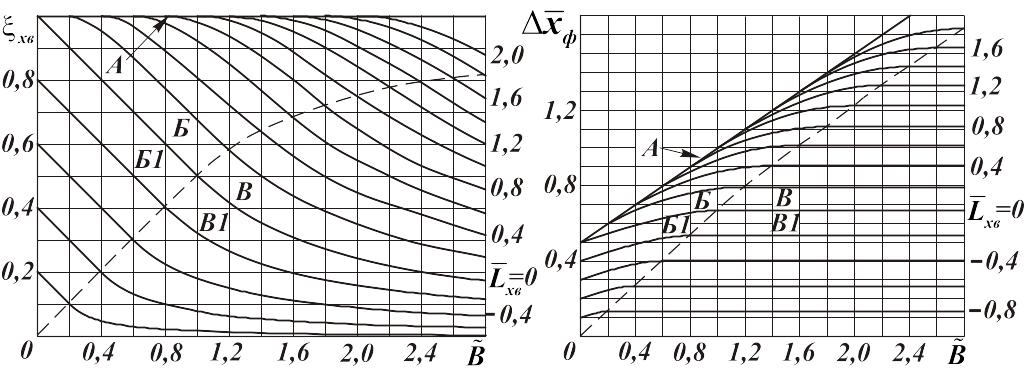

ри сверхзвуковых скоростях величину коэффициента и положение фокуса этой дополнительной подъёмной силы можно определить по графикам рис. 3.7 или по приведенным ниже формулам.

В разных областях формулы имеют различный вид:

при (рис. 3.7, область )

, (3.35 а)

; (3.35 б)

при (рис. 3.7, область )

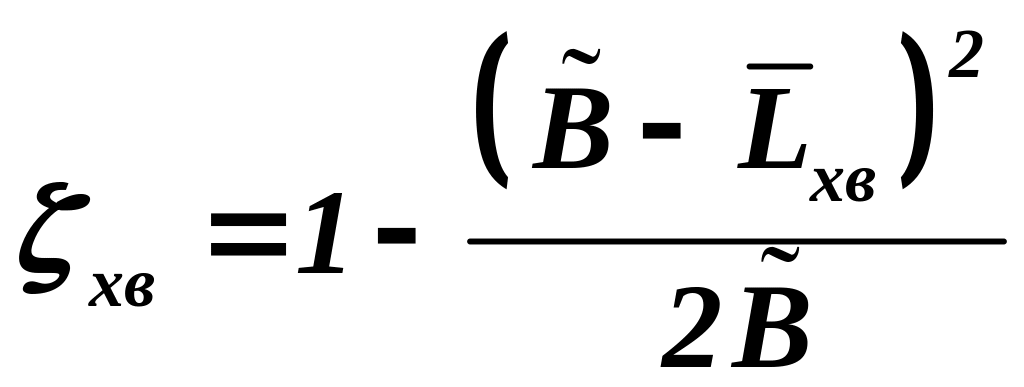, (3.36 а)

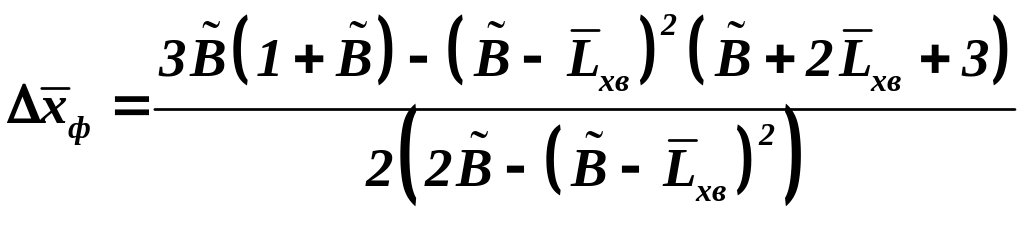; (3.36 б)

при (рис. 3.7, область )

, (3.37 а)

, (3.37 б)

где , .

На некоторых ЛА задняя кромка вторых несущих поверхностей расположена за донным срезом (см. рис. 3.6, г и д), т. е. у них . Формулы для определения величины коэффициента и положения фокуса этой дополнительной подъёмной силы при сверхзвуковых скоростях имеют следующий вид:

при (рис. 3.7, область )

, (3.38 а)

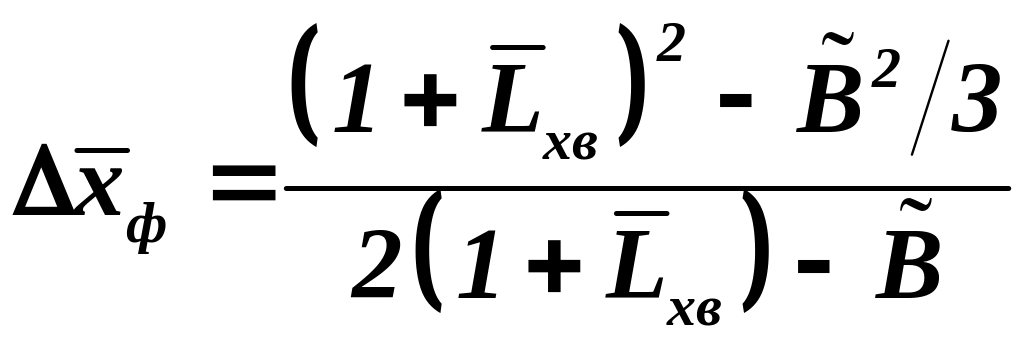; (3.38 б)

при (рис. 3.7, область )

, (3.39, а)

. (3.39, б)

При дозвуковых скоростях следует принимать значения, вычисленные по формулам (3.38, а и б) при , т. е. и .

Границы между областями на рис. 3.7 указаны пунктирными линиями. Следует ещё раз заметить, что приведенные результаты получены для плоской конфигурации ЛА с прямыми линиями Маха.

Учитывая введённые поправочные множители, выражения для определения коэффициентов интерференции корпуса и несущей поверхностью можно записать таким образом ( ):

; (3.40)

. (3.41)

Производные по углу атаки от коэффициентов дополнительных подъёмных сил, возникших из-за интерференции, согласно формуле (3.7) теперь могут быть определены так ( ):

; (3.42)

, (3.43)

где – коэффициент для -й изолированной несущей поверхности, составленной из консолей. Отсюда коэффициент для первой несущей поверхности:

. (3.44)

Таким же образом определяются аналогичные производные от коэффициентов дополнительных продольных моментов:

; (3.45)

, (3.46)

где – расстояние от носика корпуса до начала бортовой хорды консоли -й поверхности; – смещение фокуса дополнительной подъёмной силы консоли из-за влияния корпуса [8]. Это смещение невелико, и его можно определить по следующей приближённой формуле:

, (3.47)

где – размах -й несущей поверхности, составленной из консолей.

Величина в долях бортовой хорды ( ) равна при , а при сверхзвуковых скоростях определяется по графику рис. 3.7 или по соответствующим формулам (3.35) – (3.39).

Число определяется с учётом торможения потока, т. е. .