Глава 3
ПРОИЗВОДНАЯ ОТ КОЭФФИЦИЕНТА
ПОДЪЁМНОЙ СИЛЫ ПО УГЛУ АТАКИ
И ПОЛОЖЕНИЕ ФОКУСА ПО УГЛУ АТАКИ
ЛЕТАТЕЛЬНОГО АППАРАТА И ЕГО ЧАСТЕЙ
ПРИ И
Коэффициент подъемной силы и продольного момента летательного аппарата при . Центр давления и фокус по углу атаки летательного аппарата
Рассматриваемые
ЛА компонуются из корпуса большого
удлинения и несущих поверхностей обычно
малого удлинения. Для них характерно
нелинейное изменение подъёмной силы и
продольного момента по углам атаки.
Поэтому аналогичными свойствами обладают
и аэродинамические коэффициенты ЛА.
Для ЛА, обладающего горизонтальной
плоскостью симметрии, формулы для
изменение коэффициентов подъёмной силы
и продольного момента по углам атаки
удобно представить в виде суммы двух
слагаемых. Первые слагаемые (
и
)
изменяются по линейному закону от угла
атаки, а вторые (
и
)
– по почти квадратичному:
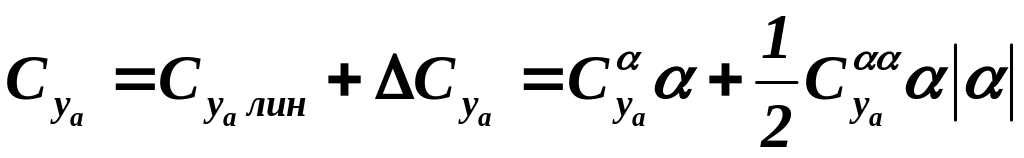; (3.1)
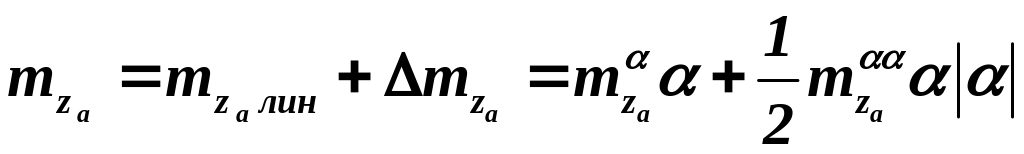. (3.2)
Здесь
и
– производные от коэффициентов подъёмной
силы и продольного момента по углу атаки
при
;
коэффициенты
и
– вторые производные по углу атаки при
.
При проектировании и «эксплуатации» ЛА удобно иметь моментные характеристики, определяемые относительно различных точек. Разработанные и используемые на кафедре аэродинамики программы расчёта аэродинамических характеристик ЛА позволяют задавать любую точку отсчёта моментных характеристик, а также характерные для ЛА длину и площадь. При аэродинамических расчётах удобно в качестве такой точки приведения выбрать фиксированную точку, связанную с телом. Для удобства изложения далее продольный момент ЛА будет определяться относительно носика корпуса, а в качестве характерной длины для него выбрана длина корпуса.
При
рассмотрении задач динамики полёта
используется система координат, начало
которой расположено в центре масс ЛА.
В качестве характерной длины иногда
удобнее использовать другой линейный
размер. Пересчёт значений коэффициента
продольного момента от одной оси
приведения к другой, а также к иному
характерному размеру выполняется очень
просто. Например, коэффициент продольного
момента
,
измеряемый от центра масс ЛА и отнесённый
к характерному размеру
,
определяется через
по следующей справедливой только при
малых углах атаки формуле:
. (3.3)
Здесь – расстояние от носика корпуса до центра масс ЛА; и – прежний и новый характерные размеры. В данных условиях предполагается, что продольный момент рассматривается только от подъёмной силы, хотя следует учитывать момент и от лобового сопротивления.
При вычислении продольного момента удобно работать с проекциями аэродинамической силы в связанной системе. В этом случае формула (3.3), но уже справедливая при любых углах атаки, для ЛА, имеющего горизонтальную плоскость симметрии, приобретает вид
.
Для решения задач, связанных с балансировкой, устойчивостью и управляемостью, необходимо знать положение центра давления и фокуса ЛА. Центром давления принято считать точку пересечения результирующей аэродинамической силы с продольной осью ЛА. Фокусом по какому-либо параметру называется точка пересечения линии приращения аэродинамической силы с осью ЛА при малом изменении этого параметра (например, угла атаки, угла поворота управляющей поверхности, высоты полёта и т. п.). Здесь будет рассматриваться только фокус по углу атаки. Вместо этого термина далее будет употребляться для краткости термин «фокус». Сказанное выше относится также к отдельным частям ЛА и их комбинациям.
Положения
центра давления
и фокуса по углу атаки
определяются по следующим формулам:
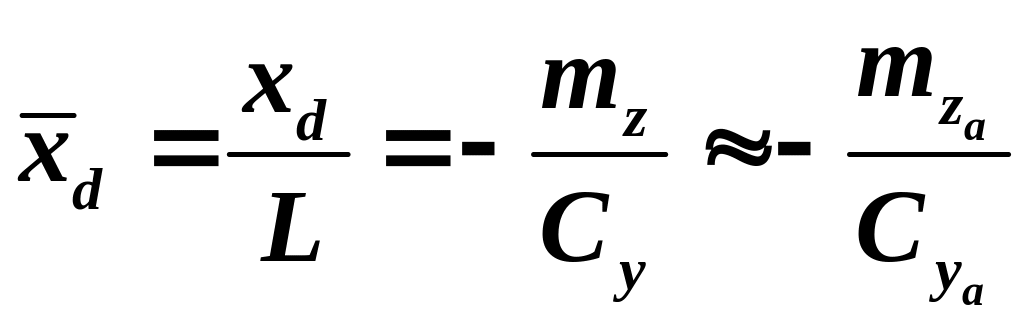; (3.4)
, (3.5)
где – характерный размер.
Как
и другие аэродинамические характеристики,
подъёмная сила ЛА определяется суммой
подъёмных сил его изолированных частей,
а также дополнительных слагаемых,
учитывающих взаимное влияние между
ними. Например,
– подъёмная сила корпуса и установленных
на нём первых несущих поверхностей
удобно представить следующим образом:
, (3.6)
где
и
– подъёмные силы изолированных корпуса
и консолей первых несущих поверхностей,
а последние два слагаемых являются
дополнительными силами, возникающими
из-за влияния корпуса на подъёмную силу
консолей (
)
и влияния консолей на подъёмную силу
корпуса (
).
Аналогичным образом можно записать
выражение и для продольного момента
этой комбинации. Эти вопросы интерференции
между частями ЛА будут рассмотрены
ниже.
В
данной главе будут рассмотрены
коэффициенты подъёмной силы и продольного
момента ЛА и его отдельных частей при
и неотклонённых рулевых поверхностях.
Эти характеристики определяются
производными от коэффициентов по углу
атаки при
.
Величины производных от коэффициентов подъёмной силы и продольного момента ЛА по углу атаки при удобно записать так:
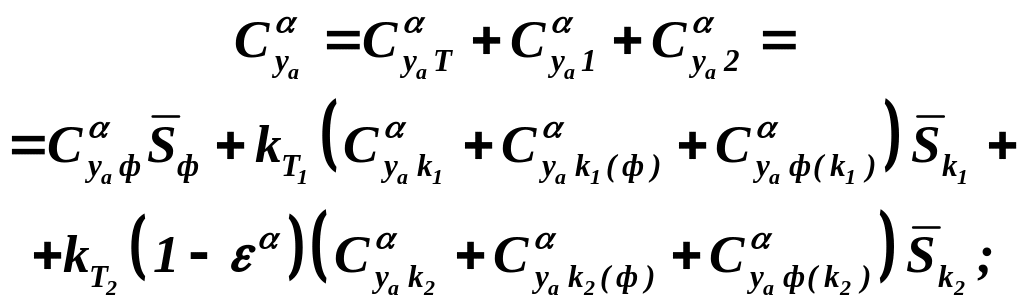(3.7)
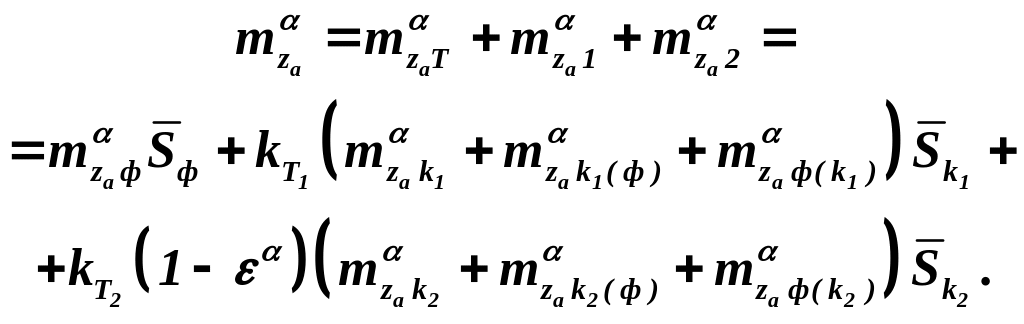(3.8)
Здесь
и
– коэффициенты торможения потока в
районе несущих поверхностей, множитель
(
)
учитывает то обстоятельство, что вторые
несущие поверхности обтекаются потоком,
скошенным вихревой пеленой, сходящей
с впереди расположенных частей ЛА;
подстрочные индексы введены по аналогии
с формулой (3.6).
Для
ЛА, имеющего горизонтальную плоскость
симметрии, при
центр давления
будет совпадать с фокусом
.
Их положение определяется по формуле
. (3.9)
Перейдём к определению величин, входящих в приведенные выше формулы.